Caos - Clase 5

Clase 5
Árboles fractales II

Esperamos tus mails en caos@oma.org.ar.

Recibimos muchos mensajes acerca de la última clase. La mayoría de los mensajes, comentaban que el tema de generar fractales con la computadora les resultaba muy interesante, pero que no tenían los conocimientos de programación necesarios.

Así que vamos a ver con más cuidado cómo funciona el programa y ver qué modificaciones se necesitan hacer para generar nuevos fractales.

(Recordamos que, en rigor, generar fractales en la computadora es imposible porque se necesitarían infinitos pasos; pero con una cantidad suficiente de pasos podemos aproximarnos muy bien.)

Para empezar, vamos a generar el mismo árbol de la clase pasada, pero usando el Cabri. (Antes habíamos comentado un mail que pedía aplicaciones en Geometre Sketchpad, que es un programa muy parecido al Cabri, así que cumplimos con el pedido.)

Para los que conozcan el Cabri, pueden ver el otro curso de OmaNet: EduCabri. En la clase 0 se ven las instrucciones básicas.

Construimos primero un segmento AB, que será el tronco del árbol:

Ahora construimos dos ramas:

Trazá las circunferencias con centro en cada vértice que pasan por el otro vértice.
Marcá las intersecciones y trazá las rectas que unen esos puntos de intersección con el vértice B.
Los ángulos que forman esas rectas con el segmento AB miden 60º.
Marcá los puntos de intersección de esas rectas con la circunferencia de centro B. Nombralos C y D.
Tomá los puntos medios de BC y BD y nombralos M y N.
Trazá los segmentos BM y BN.
Ocultá todos los objetos auxiliares, que queden únicamente los segmentos AB, BM y BN.

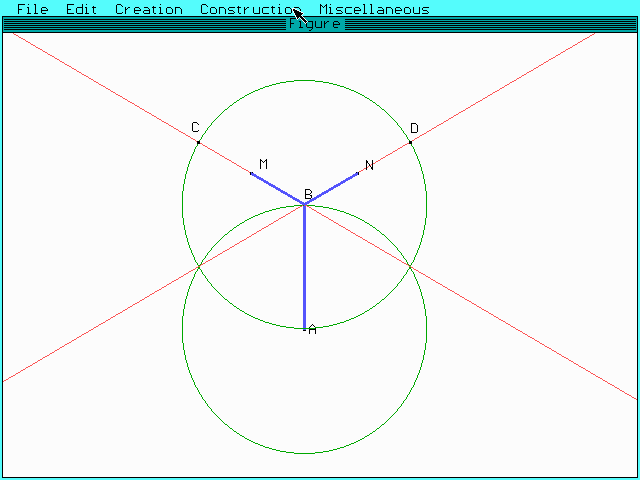
AB es el tronco y BM y BN son las primeras ramas.

La idea ahora es hacer lo mismo con BM y BN. Es decir, pensar que BM y BN son los troncos y construir las ramas que salen de estos troncos.

Los que no manejan el Cabri, se deben estar desesperando, porque seguir con esto llevaría mucho tiempo. Los que conocen el Cabri están tranquilos, porque saben que ¡existen las macros!

Lo que hacen las macros es repetir todo por nosotros. Es la misma idea que había en el programa de la clase 4, llamar siempre a la misma rutina para ir generando el árbol.

Hagamos la macro:

En el menú Miscelánea, elegí Macro Construction.
Ahora marcá New.
El objeto inicial es el segmento AB (el tronco), pero hay que tener cuidado. Si marcamos el segmento, después no vamos a saber para qué lado del segmento la macro va a construir las ramas.
Por eso, marcá como objetos iniciales primero el punto A y después el punto B.
Marcá las dos ramas (incluyendo los vértices M y N) como objetos finales.
Ponele un nombre a la macro, y ¡listo!

Ahora vamos a construir la siguiente tanda de ramas.

En el menú constuction elegí la macro que acabás de construir.
Marcá primero el punto B y después el punto M. ¿Funcionó?
Elegí de nuevo la macro, y marcá el punto B y después el punto N.
Obtenemos la siguiente figura:

Ahora podemos convertir todas las nuevas ramitas en tronquitos y así ir dandole más profundidad al árbol. Si preferís, podés hacer una nueva macro que en vez de constuirte las primeras dos ramas, te construya también las siguientes cuatro.

Después de repetir el proceso hasta cinco niveles, obtenemos la siguiente figura:

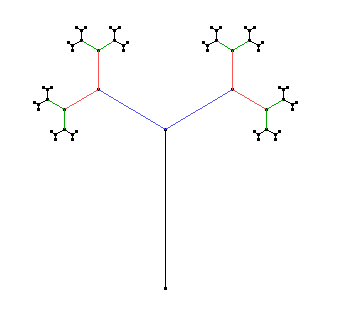
(Cada "nivel" consiste en dibujar las ramitas que sales de todas las ramas del nivel anterior.)

Hay que tener cuidado, porque el Cabri 1.7 no permite tener muchos objetos en la pantalla y entonces no podemos hacer un árbol con muchos niveles.

El programa de la clase pasada hace algo similar: cada vez que dibuja una rama, se llama a si mismo para dibujar las dos ramitas que salen de esta rama.

Por favor, hagan estos programas. En la mayoría de las escuelas se enseña algún lenguaje de programación, asi que es fácil tener acceso a los lenguajes. Cualquier lenguaje sirve. Si tienen problemas con alguna instrucción particular en algún lenguaje, pueden preguntarnos.

Nosotros estamos programando en Basic.

Es interesante pedirle al programa que se detenga después de cada rama que dibuja, para ver el orden en que va dibujando las ramas y entender mejor cómo funciona el programa.

Para esos hay que agregar la instrucción en negritas (y modificar las líneas subrayadas para que el programa corresponda exactamente con la figura que hicimos en Cabri).

DECLARE SUB rama (x1!, y1!, x2!, y2!, n!)
DECLARE SUB segmento (x1!, y1!, x2!, y2!)
SCREEN 12
CONST pi = 3.14159265#
CONST ang1 = 60 * pi / 180
CONST ang2 = 300 * pi / 180
CONST factor = .5
CONST pasos = 5
CALL rama(320, 20, 320, 220, 0)

SUB segmento (x1, y1, x2, y2)
LINE (x1, 480 - y1)-(x2, 480 - y2)
END SUB

SUB rama (x1, y1, x2, y2, n)

DO
LOOP UNTIL INKEY$=" "

CALL segmento(x1, y1, x2, y2)
x = x2 - x1
y = y2 - y1
a1 = COS(ang1) * x - SIN(ang1) * y
b1 = SIN(ang1) * x + COS(ang1) * y
a2 = COS(ang2) * x - SIN(ang2) * y
b2 = SIN(ang2) * x + COS(ang2) * y
IF (n < pasos) THEN
CALL rama(x2, y2, x2 + factor * a1, y2 + factor * b1, n + 1)
CALL rama(x2, y2, x2 + factor * a2, y2 + factor * b2, n + 1)
END IF
END SUB

En este programa tenemos que apretar la barra espaciadora para que trace cada rama.

Fijate que en vez de completar por niveles, lo que hace es después de trazar una rama trazar la ramita de la derecha y recién cuando llega al nivel 5 traza la ramita de la izquierda y vuelve a la rama anterior.

Tratemos de entender el programa.

La rutina principal son los primeros 9 renglones. Después vienen dos "sub-rutinas": SUB segmento y SUB rama.

La idea de una subrutina es que uno la puede ejecutar en cualquier momento y repite todo los pasos de la subrutina, pero con los nuevos valores con los que se llama. Es igual que una macro de Cabri.

Ahora analizamos renglón por renglón:

DECLARE SUB rama (x1!, y1!, x2!, y2!, n!)
DECLARE SUB segmento (x1!, y1!, x2!, y2!)

Estamos avisando que vamos a usar dos sub-rutinas. Entre paréntesis indicamos que valores que parametros necesitan las subrutinas.

rama necesita como parámteros los dos vertices de una rama y en qué nivel estamos, para dibujar esa rama y las ramitas que salgan de ella.

segmento necesita dos vértices de un segmento, para dibujar el segmento en la pantalla.

SCREEN 12

Cambia a modo gráfico.

CONST pi = 3.14159265#
CONST ang1 = 60 * pi / 180
CONST ang2 = 300 * pi / 180
CONST factor = .5
CONST pasos = 5

Ya vimos estas constantes en la clase pasada.

CALL rama(320, 20, 320, 220, 0)

Llama a rama para dibujar el tronco. Los cuatro primeros valores son las coordenadas del tronco y el 0 indica que estamos en el nivel 0.

SUB rama (x1, y1, x2, y2, n)

DO
LOOP UNTIL INKEY$=" "

Espera que pulsemos la barra espaciadora.

CALL segmento(x1, y1, x2, y2)

Llama a segmento para dibujar el tronco con los vertices que recibió como parametros.

x = x2 - x1
y = y2 - y1
a1 = COS(ang1) * x - SIN(ang1) * y
b1 = SIN(ang1) * x + COS(ang1) * y
a2 = COS(ang2) * x - SIN(ang2) * y
b2 = SIN(ang2) * x + COS(ang2) * y

Con estas instrucciones calcula los vértices que deben tener las dos ramitas que salen de la rama. En la clase 4 vimos de donde salen las fórmulas.

IF (n < pasos) THEN
CALL rama(x2, y2, x2 + factor * a1, y2 + factor * b1, n + 1)
CALL rama(x2, y2, x2 + factor * a2, y2 + factor * b2, n + 1)
END IF

Si todavía no alcanzó el nivel pedido, se llama a si misma para dibujar las dos ramitas que salen de la rama. Fijate que entonces, cuando quiera trazar estas dos ramitas, se va a volver a llamar a si misma para trazar las ramitas que salgan de las ramitas.

END SUB

Termina la subrutina rama

SUB segmento (x1, y1, x2, y2)
LINE (x1, 480 - y1)-(x2, 480 - y2)

Dibuja en la pantalla el segmento con los vértices que recibe.

END SUB

Termina la subrutina segmento.

¿Se entendió? Vuelvan a pnesar los problemas que les dimos en la clase 4, a ver si salen.

Este es muy parecido al anterior. Solo hay que cambiar la constante factor y las constantes ang1 y ang2. ¿Qué valores habrá que darles? Acordate que el ángulo que estamos midiendo es el que forma la prolongación del tronco con cada una de las ramas.

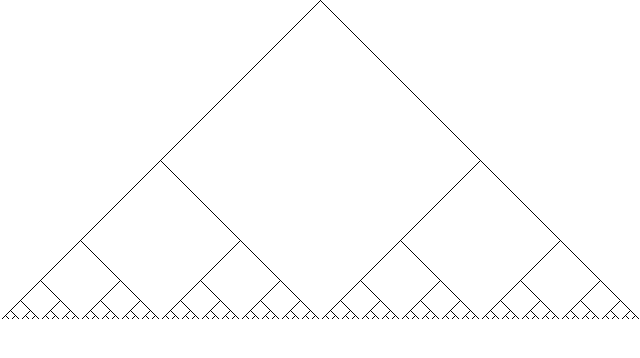
En este la cosa es distinta. Las principales diferencias son que no hay tronco y que el ángulo de cada ramita no depende de la rama anterior, siempre es de 135º o de 225º con respecto al eje Y.

Entonces un programa posible es:

DECLARE SUB rama (x!, y!, largo!, n!)
DECLARE SUB segmento (x1!, y1!, x2!, y2!)
SCREEN 12
CONST factor = .5
CONST pasos = 10
CALL rama(320, 400, 160, 0)

SUB rama (x, y, largo, n)
CALL segmento(x, y, x + largo, y - largo)
CALL segmento(x, y, x - largo, y - largo)
IF (n < pasos) THEN
        CALL rama(x + largo, y - largo, largo * factor, n + 1)
        CALL rama(x - largo, y - largo, largo * factor, n + 1)
END IF
END SUB

SUB segmento (x1, y1, x2, y2)
LINE (x1, 480 - y1)-(x2, 480 - y2)
END SUB

Entiendanlo antes de hacerlo. Fijense que ahora el cálculo de los ángulos se simplificó mucho. Porque si el vértice superior de una rama es (x, y) entonces el vertice inferior va a ser (x + largo, y - largo) o (x - largo, y - largo).

Ejercicios

1. Hacer la siguiente fiugra en Cabri

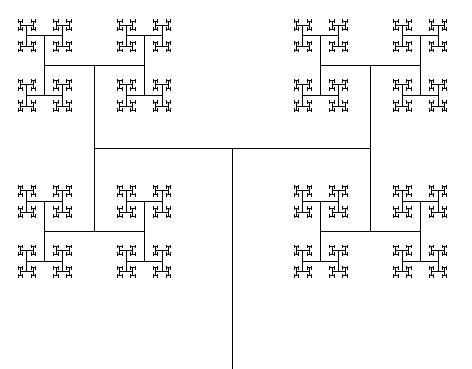
2. Hacer un programa que realice la siguiente figura:

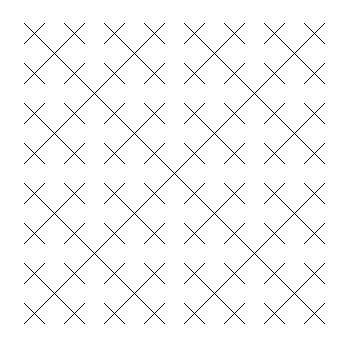
La figura anterior tiene 3 niveles de profundidad. Si le pedimos 5 niveles, obtenemos el siguiente gráfico:

Probá pedirle 8 o más niveles, y ¡te vas a llevar una gran sorpresa!

Así terminamos la quinta clase de Caos, el curso sobre caos y fractales de Omanet. Esperamos que te haya gustado. Próximamente ofreceremos una nueva clase.

Mientras tanto es tu turno. Queremos que sigas las actividades y nos cuentes lo que conseguiste y las cosas que te hayan surgido. Envía tus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es caos@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

(Todos los campos son opcionales, pero te pedimos que nos des tu dirección de mail si nos dejás alguna pregunta o comentario.)

Caos OmaNet Página principal	OmaNet - Educación Interactiva www.oma.org.ar/omanet \| omanet@oma.org.ar
mensajes webmaster@oma.org.ar