Clase 4
Árboles fractales

 

Esperamos tus mails en caos@oma.org.ar.

Volvemos ahora a los fractales. Como ves, el curso es un poco desorganizado, va saltando de tema en tema. Te pedimos disculpas, pero nos pareció mejor. No queremos agotar ningún tema, porque sobre cualquier tema siempre hay mucho para decir. Entonces vamos a ir desarrollándolos según el interés de nuestros lectores.

Al final de cada clase, agregamos una encuesta. ¡Completenla siempre! El curso lo hacemos para ustedes, queremos saber que hay gente del otro lado y su opinión sobre el curso. Para nosotros es, de verdad, muy importante que la completen.

Como ya habrás descubierto, las computadoras juegan un papel vital en la teoría de los fractales. En esta clase vamos a hacer un programa para dibujar "árboles".

La OMA editó un libro muy bueno sobre fractales: Un paseo por el jardín de los fractales, de Néstor Aguilera. Vamos a seguir algunas ideas de sus ideas. El libro usa como lenguaje el Mathematica, un soft muy recomendado.

Nosotros vamos a programar en Basic, para que más gente pueda aprovecharlo. Pero es muy fácil traducir las cosas a cualquier lenguaje (Pascal, C, Mathematica o incluso las calculadoras programables). Te pedimos que cualquier programa que hagas en cualquier lenguaje nos lo mandes, para que todos puedan aprovecharlo.

Una de las observaciones de Mandelbrot (el padre de los fractales) es que la Naturaleza muchas veces tiene un comportamiento iterativo en sus formas, en escala cada vez menor. Es lo que podemos ver un tanto idalmente, en las ramificaciones de los árboles. No, los árboles no son fractales, pero las ideas que desarrollamos en esta clase nos aproximan bastante.

La idea es simple. Empezamos con un tronco. Del tronco salen dos ramas. De cada una de las ramas salen dos nuevas ramas, y así sucesivamente.

Obtenemos un dibujo como este:

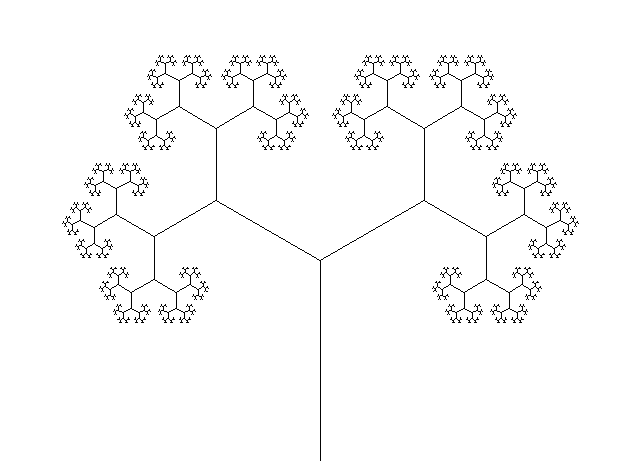
Veamos cómo hacer el programa:

Si miramos una de las dos ramas principales, vemos que es identica al árbol pero rotado.

Entonces vamos a necesitar saber rotar un segmento. En una primer lectura, podés saltear esta parte.

Ponemos coordenadas, y queremos rotar el vector (x,y). (O equivalentemente, el segmento de vértices (0,0) y (x,y) con centro de rotación en el punto (0,0) )

Suponemos primero que el vector tiene longitud 1 y queremos rotarlo alfa grados.

Queremos obtener un vector (a,b) como en la figura:

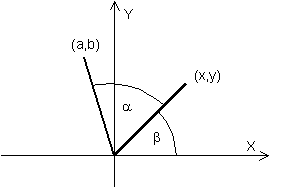
Como (a, b) también tendrá longitud 1, por trigonometría, sabemos que

a = cos (alfa + beta)
b = sen (alfa + beta)

Usando las fórmulas de coseno y seno de una suma de ángulos, obtenemos:

a = cos (alfa) * cos (beta) - sen (alfa) * sen (beta)
b = sen (alfa) * cos (beta) + cos (alfa) * sen (beta)

Pero sabemos que

x = cos (beta)
y = sen (beta)

Entonces

a = x * cos (alfa) - y * sen (alfa)
b = x * sen (alfa) + y * cos (alfa)

Estas son las fórmulas que buscábamos.

Para hacer el programa creamos una subrutina que dibuja una rama con las coordenadas dadas y se llama a si misma para dibujar las dos ramificaciones. Esto es un programa recursivo, cada vez se vuelve a llamar a si mismo y se van creando las ramificaciones. Después de una cantidad fija de ramificiones el programa para.

La primera vez la llamamos con las coordenadas del tronco, y automáticamente se construye todo el árbol.

El programa es el siguiente:

DECLARE SUB rama (x1!, y1!, x2!, y2!, n!)
DECLARE SUB segmento (x1!, y1!, x2!, y2!)
SCREEN 12
CONST pi = 3.14159265#
CONST ang1 = 60 * pi / 180
CONST ang2 = 300 * pi / 180
CONST factor = .6
CONST pasos = 10
CALL rama(320, 20, 320, 220, 0)

 

SUB segmento (x1, y1, x2, y2)
LINE (x1, 480 - y1)-(x2, 480 - y2)
END SUB

 

SUB rama (x1, y1, x2, y2, n)
CALL segmento(x1, y1, x2, y2)
x = x2 - x1
y = y2 - y1
a1 = COS(ang1) * x - SIN(ang1) * y
b1 = SIN(ang1) * x + COS(ang1) * y
a2 = COS(ang2) * x - SIN(ang2) * y
b2 = SIN(ang2) * x + COS(ang2) * y
IF (n < pasos) THEN
   CALL rama(x2, y2, x2 + factor * a1, y2 + factor * b1, n + 1)
   CALL rama(x2, y2, x2 + factor * a2, y2 + factor * b2, n + 1)
END IF
END SUB

 

Screen 12 pone la pantalla en resolución 640 * 480. Si usan otra resolución van a tener que cambiar algunos valores en el programa.

Las constantes ang1 y ang2 son los ángulos con que se rota una rama para obtener las dos ramificaciones. Pueden probar darle otros valores para obtener nuevos fractales. Los ángulos están en radianes. Si quieren dar los ángulos en grados, simplemente cambien los número 60 y 360 por los ángulos en grados que quieran.

La constante factor es la razón entre la longitud de una rama y la longitud de sus ramificaciones. La constante pasos indica la cantidad de ramificaciones del árbol. También pueden modificarlas.

La subrutina segmento cambia las coordenadas a las coordenadas del plano. Esto hay que hacerlo porque en Basic, el punto (0,0) es el punto superior izquierdo de la pantalla y no el inferior izquierdo como querríamos.

La subrutina rama es la parte principal del programa. Dibuja una rama con los vértices que recibe, y se llama a si misma para dibujar las dos ramificaciones.

La nuevas ramas empiezan donde terminaba la rama anterior ( (x2,y2) ) y terminan en ese punto más el vector rotado en ángulos ang1 y ang2 y reducido según la constante factor.

Por cada ramificación aumenta n en 1 y cuando n llega a la cantidad de ramificaciones indicadas en paso, para.

No quisimos explicar con mucho detalle el programa, para no hacer densa la clase, pero por favor escríbannos si hay algo que no entienden. Así van a poder hacer sus propios fractales muy fácilmente.

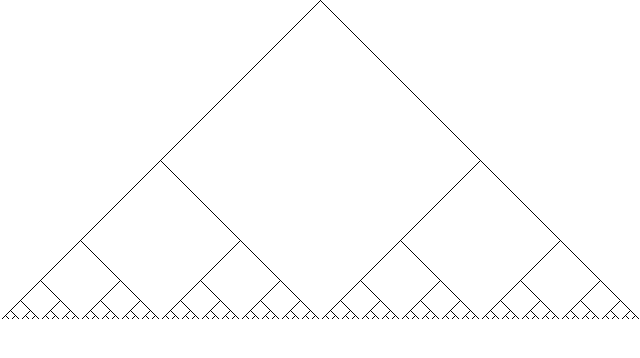
Como ejercicio, les pedimos que hagan progamas para reproducir los siguientes fractales:

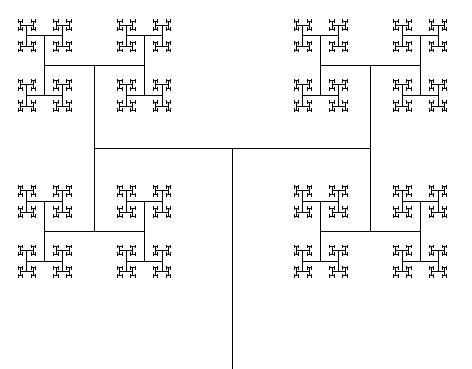
El anterior se hace simplemente modificando los ángulos. En el que viene van a tener que modificar las instrucciones del programa:

Así terminamos la cuarta clase de Caos, el curso sobre caos y fractales de Omanet. Esperamos que te haya gustado. Próximamente ofreceremos una nueva clase.

Mientras tanto es tu turno. Queremos que sigas las actividades y nos cuentes lo que conseguiste y las cosas que te hayan surgido. Envía tus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es caos@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

(Todos los campos son opcionales, pero te pedimos que nos des tu dirección de mail si nos dejás alguna pregunta o comentario.)

Caos OmaNet   Página principal	OmaNet - Educación Interactiva    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar