Clase 1
Introducción a los fractales

 

Esperamos tus mails en caos@oma.org.ar.

Bienvenidos a Caos, el curso de Omanet dedicado a los fractales y el caos. En esta primera clase, haremos una breve introducción a los fractales. En la próxima clase hablaremos un poco sobre qué es la teoría del caos. Luego, seguiremos desarrollando estos dos temas, y descubriendo la relación entre ellos.

Los algoritmos iterativos van a jugar un papel muy importante, así que iremos mostrando aplicaciones en Derive, o en una calculadora gráfica o en algún lenguaje de programación.

El 7 de abril comienza una residencia en Rosario sobre este tema. Va a haber cursos para todos los niveles, para alumnos secundarios, estudiantes universitarios, terciarios, de profesorado y graduados. ¡No se lo pierdan! Hay mas información en www.oma.org.ar/actividades/residencia3.htm

En próximas clases, vamos a incluir parte del material de esos cursos, y proponer actividades para los que asistieron, de modo que sigan profundizando.

Para entender lo que es un fractal, vamos a comenzar por un ejemplo sencillo: el triángulo de Sierpinski.

1. Empezamos con un triángulo equilátero (relleno).

2. Tomamos los puntos medios de sus lados, y trazamos el triángulo formado por ellos. Quitamos este triángulo de la figura original.

3. La figura está compuesta ahora por 3 triángulos más chicos. Hacemos lo mismo en estos tres triángulos.

4. Ahora tenemos 9 triángulos, y podemos hacer lo mismo en cada uno de estos triángulos.

5. Si repetimos este proceso indefinidamente vamos a obtener lo que se conoce como el triángulo de Sierpinski. Para formalizar bien lo último, tenemos que meternos con nociones de límite. Pero por ahora, la idea intuitiva va a estar bien. La figura es aproximadamente así:

Esta figura que obtuvimos es un fractal.

La principal característica de nuestra figura es la "auto-semejanza".

Si en la figura final miramos un triangulito, este triángulo es exactamente igual al original, sólo que más chiquito. Cuando una figura tiene esta característica, decimos que posee auto-semejanza.

Una observación importante es que necesitamos repetir el proceso infinitas veces para obtener la autosemejanza. Si lo hiciésemos por ejemplo 10 veces, y miramos uno de los tres triángulo que se forman en la primera etapa lo que vamos a ver no es exactamente igual a la figura original porque habría que sacarle todavía unos triangulitos para que sean iguales.

Algunas preguntas:

1. ¿Cuántos triangulitos quedan formados en la etapa n?
2. ¿Cuantos triangulitos quitamos en la etapa n?
3. Si suponemos que el triángulo original tiene área 1, ¿qué área tendrá la figura luego de quitar el primer triangulito?
4. ¿Qué área tendrá la figura después de n etapas?
5. ¿Qué área tendrá la figura después de repetir el proceso infinitas veces?

¡La respuesta a la última pregunta es sorprendente! Vamos a hablar mucho sobre ese tema en las próximas clases.

¿Qué pasaba si en vez de tomar un triángulo equilátero tomábamos otro triángulo? Podemos hacer lo mismo, y va a seguir cumpliendo la propiedad de auto-semejanza. Obtendríamos algo como en la figura:

Tratá de pensar ahora qué podemos hacer en un cuadrado. Hay varias posibilidades, vamos a ver una. Si se te ocurre otra cosa, por favor escribinosm, así la mostramos.

1. Comenzamos con un cuadrado.
2. Si tomamos los puntos medios, y quitamos el cuadrado que forman, no sabemos como seguir, porque no obtenemos cuadraditos más pequeños.
3. Una posibilidad es, entonces, dividir al cuadrado en nueve cuadraditos y quitar el del centro. Es similar al triángulo de Sierpinski, si pensamos que lo dividíamos en cuatro triangulitos y quitábamos el del centro.

4. Ahora hacemos lo mismo para cada uno de los 8 cuadraditos.
5. Repitiendo este proceso infinitas veces, obtenemos algo como la figura.

6. Si en la figura final, miramos alguno de los 8 cuadraditos que se formaron en la primer etapa, éstos son exactamente iguales al original, sólo que más pequeños. Por lo tanto, esta figura también posee auto-semejanza.

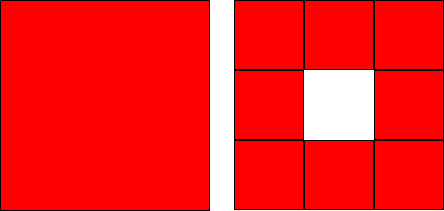
Nos vamos a conformar por ahora con estos dos ejemplos. En las próximas clases vamos a dar más ejemplos, para llegar a definir con precisión qué es un fractal.

Antes de despedirnos, vamos a dar un algoritmo muy simple para para obtener una figura similar al triángulo de Sierpinski, pero por un método totalmente distinto.

Que el resultado sea el mismo es realmente increíble y es parte de lo que hace que los fractales sean tan interesantes.

El algoritmo es el siguiente:

1. Tomamos tres vértices de un triángulo.
2. Marcamos un punto cualquiera en el interior del triángulo.
3. Elegimos un vértice del triángulo al azar, y marcamos el punto medio entre el vértice elegido y el punto marcado.
4. Elegimos otro vértice al azar (puede resultar de nuevo el mismo) y marcamos el punto medio entre el vértice marcado y el último punto marcado.
5. Repetimos el punto 4 indefinidamente.

Para poder tener una idea del resultado, necesitamos hacerlo muchas veces. Por eso, es necesario una computadora o una calculadora.

Esta es la implementación en una calculadora gráfica Casio. Tomamos como vértices del triángulo los puntos (0;0), (0;1) y (1;0).

Range 0,1,1,0,1,1
0.5 -> I
0.5 -> J
Lbl 1
Int (2Ran#)-> X
Int (2Ran#)-> Y
XY = 1 => Goto 1
2^-1(I+X)-> I
2^-1(J+Y)-> J
Plot I,J
Goto 1

La siguiente figura se obtuvo con el mismo algoritmo en QBasic:

Así terminamos la primer clase de Caos, el curso sobre caos y fractales de Omanet. Esperamos que les haya gustado. Dentro de dos semanas ofreceremos una nueva clase.

Mientras tanto es tu turno. Queremos que sigas las actividades y nos cuentes lo que conseguiste y las cosas que te hayan surgido. Enviános tus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es caos@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

Caos OmaNet	OmaNet - Educación Interactiva    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar