XI OLIMPÍADA PROVINCIAL DE ENTRE RÍOS - 2007
 

Primer Nivel

Problema 1. Decidir si es posible armar un rectángulo de 39 ´ 44 sin huecos ni superposiciones, usando exclusivamente piezas rectangulares de 5 ´ 11. ¿Y si el rectángulo que se quiere armar es de 42 ´ 55?

En cada caso, si la respuesta es afirmativa, dar un ejemplo y en caso contrario, explicar por qué.

ACLARACIÓN: En todos los casos está permitido girar las piezas.

Problema 2. Sea ABC un triángulo tal que  y . Se marca en el lado AB el punto D tal que . Se traza por D la paralela a BC, que corta a AC en L. Determinar la medida del ángulo .

Problema 3. Se tienen 8 monedas, todas de igual aspecto, entre las hay monedas falsas. Se sabe que hay al menos una moneda auténtica y al menos una falsa. Todas las monedas auténticas tienen el mismo peso, y todas las falsas tienen igual peso. Las falsas son más livianas que las auténticas. Demostrar que es posible determinar la cantidad de monedas falsas, usando a lo sumo 5 veces una balanza de dos platos.

ACLARACIÓN: En cada pesada, la balanza de platos compara los pesos de los objetos colocados en los platos y establece si el peso de los objetos de un plato es igual, menor o mayor que el peso de los objetos colocados en el otro plato.

Segundo Nivel

Problema 1. En el tablero de 4 ´ 4 se han escrito, en clave, los números naturales desde el 5 al 20 inclusive, sin repetir. La suma de los cuatro números de cada fila y la suma de los cuatro números de cada columna es siempre la misma. Además, el número de la casilla superior izquierda es impar. Cada letra representa un dígito distinto y letras diferentes representan dígitos diferentes. Determinar a qué dígito corresponde cada letra.

Problema 2. Tres ciclistas Axel, Bruno, César corren alrededor de una pista circular. Los tres salen al mismo tiempo, desde el mismo lugar de la pista y en el mismo sentido, y los tres se detienen al mismo tiempo cuando están todos nuevamente en un mismo lugar de la pista. Durante la práctica, César pasó 20 veces a Axel. Determinar cuántas veces un ciclista pasó a otro a lo largo del entrenamiento, si se sabe que César es más veloz que Bruno y Bruno es más veloz que Axel.

Problema 3. Demostrar que todo triángulo se puede cortar en 4 triángulos isósceles (no necesariamente iguales).

Tercer Nivel

Problema 1. Calcular el valor de la expresión

donde se han multiplicado las 99 fracciones de la forma  para todos los enteros k desde 2 hasta 100 inclusive.

Problema 2. Pablo debe resolver el siguiente problema sin usar calculadora ni trasportador:

En una hoja cuadriculada se marcaron los puntos A, B, C, D, E, como muestra la figura. Sean  y . Hallar el valor de .

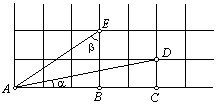
¿Cómo puede hacerlo?

Problema 3. Hay 18 toneladas de mercadería distribuida en paquetes de pesos desconocidos. El número total de paquetes es mayor que 35. La mercadería se debe transportar en 7 camiones que pueden cargar a lo sumo 3 toneladas cada uno. Se sabe que estos 7 camiones pueden transportar, entre los 7 y en un solo viaje, cualquier conjunto de 35 de los paquetes. Demostrar que los 7 camiones pueden transportar, entre los 7 y en un solo viaje, toda la mercadería.

Olimpíada Matemática Argentina Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar