
8va Competencia
de Clubes Cabri
Primera Ronda
26 de junio al 6 de julio de 1998
| nivel A |
1
Construir la siguiente figura donde ABCDEF y A’B’CD’EF’ son hexágonos regulares.

2
¿Si el área de CDED’ es 5, cuál es el area de GA’HA? Justificar.
3
¿Qué perímetro es mayor: el del hexágono ABCDEF o el del triángulo AGA’? Justificar.
4
Construir una circunferencia C de centro O, luego un punto P en ella. Construir un punto Q en C de forma tal que el ángulo QPO mida 60°. Construir un punto R en C de forma tal que el ángulo RPO mida 45° y QPR sea agudo. (Recordar que todas las construcciones deben justificarse con pasos hechos con regla y compás.) Sea S la intersección entre PR y QO. ¿Cuánto mide el ángulo QSP? Justificar.
5
En el problema anterior, sea r la recta perpendicular a PO que pasa por P y sea T la intersección entre r y QO. Hallar el área del triángulo POT si el radio de la circunferencia es 8.
| nivel B |
6
Dados un segmento AB y un punto cualquiera P en el segmento AB, construir la figura, donde ABCDEF es un hexágono regular y C1 = C3 = C5 y C2 = C4 = C6.
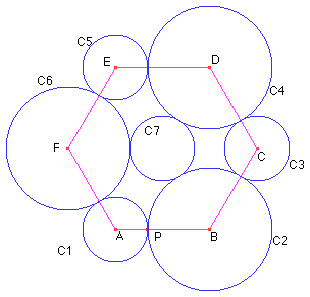
7
Probar que en el problema anterior C7 = C5 = C3 = C1.
8
Dividir un cuadrado ABCD en 6 rectángulos iguales. (Recordar que la figura no debe deformarse al mover A, B, C o D.)
9
¿De cuantas formas se puede dividir a un cuadrado en 12 rectángulos iguales?
10
Dado un triángulo ABC, sea P un punto en AC. Sean O1 y O2 los circuncentros de los triángulos ABP y PBC respectivamente. Probar que los ángulos ABC y O1PO2 miden lo mismo.
| nivel C |
11
¿Cuáles son todas las formas de dividir a un cuadrado en 6 rectángulos iguales?
12
Dado un hexágono regular ABCEDF, se construye los simétricos de A con respecto a las rectas BC, CD, DE y EF que llamamos G, H, I y J respectivamente. Hallar la relación entre las áreas de GHIJ y ABCDEF.
13
Dado un paralelogramo ABCD se trazan las bisectrices de sus ángulos formandose con las intersecciones entre las bisectrices un nuevo cuadrilátero IJKL. ¿Qué tipo de cuadrilátero es IJKL?
14
¿Cómo debe ser ABCD para que IJKL sea un cuadrado?
15
Sea ABC un triángulo y sea D un punto en AC. Se traza C1, la circunferencia de centro A que pasa por D y corta a AB en E. Se traza C2 circunferencia de centro B que pasa por E y corta a BC en F. Se traza C3, la circunferencia de centro C que pasa por F y corta a CA en G. Hallar el lugar geométrico del punto medio de DG al variar D sobre AC.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |