Décimo-Novena Competencia de Clubes Cabri
Soluciones de la Primera Ronda

Nivel Menor

Problema N°1:

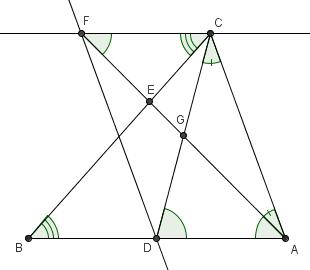
Dado un triángulo acutángulo ABC se marcan el punto D en BC y el punto E en AC, de forma que AEB=ADB=90°. Las bisectrices de los ángulos CAD y CBE se cortan en F. Hallar el ángulo AFB.

Solución 1 de "Los Salamitroskys Reloaded" y "Parro2008A":

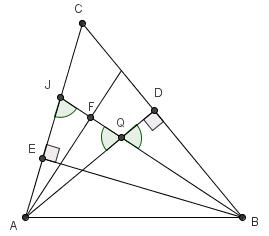
Sean J y Q las intersecciones de BF con AC y AD respectivamente.


Si miramos los triángulos BEJ y BDQ, como JBE = QBD y BEJ = BDQ = 90º entonces EJB = DQB. Pero DQB = AQJ de donde EJB = AQJ.
Si ahora miramos los triángulos AFJ Y AFQ, como JAF = QAF y AJF = AQF entonces AFJ = AFQ.
Luego AFJ = AFQ = 180º/2 = 90º. Es decir que AFB = 90º.

Solución 2 de "Las Chicas Geométricas"

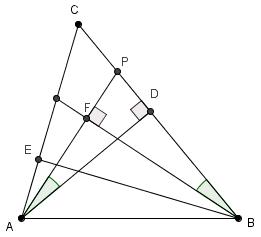
Notemos que DAP = ½ DAC = ½ CBE = FBP ya que DAC = 90 – ACB = CBE. Luego, si miramos los triángulos APD y BPF tenemos que DAP = FBP y que APD = BPF de donde PDA = PFB, es decir AFB = PFB = 90º.

Solución 3 de "Cuadrados al Cubo"

Se tiene que

Y análogamente Entonces AFB = 180º - FAB - FBA
AFB = 180º - (135º- ½ ACB - ABC) - (135º - ½ ACB - CBA)
AFB = ABC + CBA + ACB - 90º =180º- 90º =90º



Problema N°2:

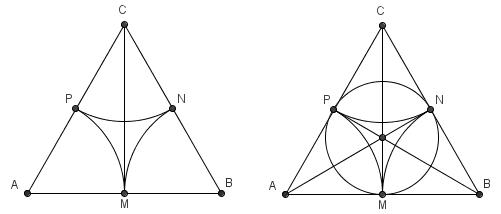
Sea ABC un triángulo equilátero de lado 2 y sean M, N y P los puntos medios de AB, BC y CA respectivamente. Se trazan las tres circunferencias de radio 1 con centro en A, B y C.
a) Calcular el área de la región sombreada en la figura A.
b) Se traza la circunferencia que pasa por M, N y P. Calcular el área de la región sombreada en la figura B.

Solución de "Clockwork":

a)

  • Primero calculamos la altura del triángulo ABC: al trazarla sobre el lado AB, queda formado un triángulo rectángulo de hipotenusa AC y base AM. Usando Pitágoras tenemos la ecuación:
    AM ² + MC ² = AC ².
  • Reemplazamos AM por 1 y AC por 2 y queda
    1 + MC ² = 4, con lo que MC = √3
  • De esta manera calculamos el área del triángulo ABC:
    Área (ABC) =2. √3 /2= √3
  • Seguimos con el área de los sectores circulares, éstos son de 60º (pues el triángulo es equilátero) y de radio 1 luego:
    Área sector circular de 60º y radio 1 = π.1².60º /360º= 1/6 π.
    Por último al área del triángulo le restamos el área de los 3 sectores circulares y queda:
    Area Figura A = √3 -3.1/6. π =√3 – 1/2 π = 0,1612...

    b)
  • El radio del círculo trazado es igual a la apotema del triángulo ABC. Tomando el perímetro del triángulo (2.3=6) y el área del triangulo ABC calculada anteriormente, realizamos la siguiente ecuación:
    6.apotema / 2=√3.
  • Despejando, apotema = 1/3 √3.
  • Calculamos el área del círculo trazado que es: π.(1/3 √3)^2 = 1/3 π.
  • Por último al área del circulo le restamos el área obtenida en la parte A:
    Área Figura B = 1/3 π – (√3 - ½ π) = 5/6 π – √3 = 0,8859...



    Problema N°3:

    Sea ABC un triángulo. Sea D el punto medio de AB y sea E un punto en el segmento BC tal que BE=2.EC. Sabiendo que los ángulos BAE y ADC son iguales, hallar el ángulo BAC.

    Solución de "Life is GREEN!"

    Sea r la paralela a AB por C y llamemos F a su intersección con la prolongación de AE.
    El triángulo AEB es semejante al FEC ya que tienen los mismos ángulos, luego AB/FC = BE/EC = 2. Es decir que AB = 2 FC, pero D es el punto medio de AB, entonces AD = DB = FC.


    El cuadrilátero ADFC tiene lados opuestos iguales y paralelos (AD y FC), de donde ADFC es un paralelogramo. Si G es la intersección de sus diagonales entonces DG = GC (ya que las diagonales de un paralelogramo se cortan en su punto medio) y DG = GA (pues por el dato del problema el triangulo AGD es isósceles). Luego DG = GA = GC.
    Por ultimo, GCA = GAC (pues GC = GA) y ADG = DAG (dato del problema), pero
    DAC = DAG + GAC
    DAC = ½ (DAG + ADG + GAC + GCA)
    DAC = ½ (ADG + GCA + DAC)
    DAC = ½ (180º) = 90º
    Es decir que BAC = DAC = 90º.