Problema N°1:

Sea P un punto interior al triángulo ABC tal que la recta AP es la bisectriz del ángulo BAC, BP es la bisectriz de ABC y CP es la bisectriz de ACB. Si APB=110º, BPC=120º y CPA=130º, hallar los ángulos del triángulo ABC.

 

 

Solución de “Binomius”:

 

  El punto P es la intersección de las tres bisectrices del triángulo ABC, por lo que este punto será el incentro del triángulo.

  La bisectriz de cada ángulo del triángulo ABC divide a cada uno de ellos en dos ángulos iguales, por lo que:

 

<BAC=2<BAP =2<PAC

<ABC=2<ABP =2 PBC

<ACB=2<ACP =2<BCP

 

Para simplificar los cálculos, escribimos:

 

<BAC= 2α

<ABC= 2β

<ACB= 2γ

 

Por la propiedad de los ángulos interiores de un triángulo, sabemos que:

2α+2β+2γ= 180º de donde   α+β+γ= 90º (1)

 

Por la propiedad de los ángulos interiores de los triángulos, en los triángulos PAB, PAC y BPC respectivamente:

 

β+α+110º= 180º à  β+α=70º     (2)

α+γ+130º= 180º à  α+γ=50º      (3)

β +γ+120º= 180º à  β +γ=60º    (4)

 

Reemplazando (2), (3) y (4) en (1) obtenemos los valores de α, β y γ.

(2) en (1): 70º+γ = 90º    de donde γ=20º

(3) en (1): 50º+β=90º     de donde β=40º

(4) en (1): 60º+α=90º     de donde α=30º

 

De esta manera, los ángulos del triángulo ABC son:

<BAC= 2α =2 . 30º = 60º

<ABC= 2β = 2 . 40º = 80º

<BCA= 2γ = 2 . 20º = 40º

 

Respuesta: Los ángulos del triángulo ABC son <BAC= 60º, <ABC= 80º, <BCA= 40º.

 

Problema N°2:

Sea ABCD un paralelogramo. Marcamos el punto medio de CD, al que llamamos M. Llamamos P a la intersección de BC con la recta AM. Se sabe que AM es la bisectriz del ángulo BÂD y que PB=10. Hallar el perímetro del paralelogramo ABCD.

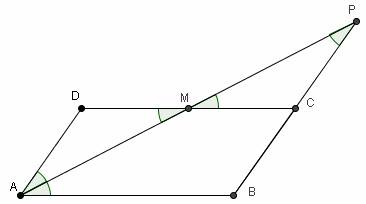
Solución de “Los CJS”: 

 

   El perímetro del paralelogramo ABCD es 30. Teniendo en cuenta los datos dados, sacamos estas conclusiones:

 

<BAM = <DMA por ser alternos internos

<BAM = <DAM, porque el segmento AM es bisectriz del ángulo <A

 

De donde   <DAM = <DMA y el triangulo ADM resulta isósceles en D.

 

AD=DM por ser ADM un triangulo isósceles.

DM=MC por ser M punto medio de DC.

AD=BC por ser lados opuestos del paralelogramo ABCD.

 

De donde AD =DM =MC =BC.

 

DM=CM por ser M punto medio de DC.

<DMA=<PMC, por opuestos por el vértice.

<ADM=<PCM, por ser alternos internos entre paralelas.

 

De donde el triangulo ADM es igual a PCM, porque tienen un lado igual (DM=CM) y los dos ángulos adyacentes a él son iguales (<DMA=<CMP, y <ADM=<PCM).

 

Entonces PC=AD=DM=CM. Es decir:

 

PC=CM=AD=DM=BC.

 

Si PB=10, entonces BC + CP=10 pero BC=CP, y concluimos BC=5, es decir

 

PC=CM=AD=DM=BC=5.

 

Y como AB=CD=CM+DM =5+5=10, luego AB=CD=10 y AD=BC=5,

 

AB + BC + CD + AD = 10+5+10+5 = 30

 

Respuesta: El perímetro del paralelogramo ABCD es 30.

 

Problema N°3 (corregido):

Sea ABCD un cuadrado de lado 1. Se marcan P, Q, R y S interiores al cuadrado y tales que ABP, BCQ, CDR y DAS sean triángulos equiláteros.

 
a) Hallar el área del cuadrilátero PQRS.

b) Si se borran todos los elementos de la figura excepto los puntos P, Q, R y S, indicar un procedimiento para reconstruir el cuadrado ABCD, usando sólo regla y compás.

 

Solución de “Los discípulos de Maite”:

 

Vamos a demostrar que los triángulos QDP, PCS, SBR y RAQ son equiláteros.

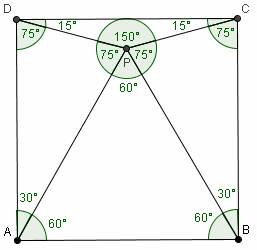
·         Como ABP es equilátero entonces BAP=60° y PAD= 90°-60°=30°

·         Como AD=AB=AP luego DAP es isósceles, ADP=APD= (180°-30°)/2=75°

·         De lo anterior PDC= ADC-ADP de donde PDC= 90º-75º= 15º y análogamente PCD=15º

·         El triangulo CPD resulta isósceles en P con DPC= 180º-PDC-PCD es decir que DPC=180º-15º-15º=150º.

·         Análogamente QDA=QAD=15° y AQD=150° luego los triángulos AQD y CPD son congruentes ya que tienen los mismos ángulos y AD=CD por lo tanto tenemos que QD=PD.

·         Pero QDP=ADC-ADQ-PDC, es decir que QDP=90º-15º-15º=60º

·         Como DQ=QP entonces QDP es isósceles en D con QDP=60º, de donde DQP=DPQ= (180°-60°)/2=60°.

·         Por lo tanto el triángulo QDP es equilátero.

·         Análogamente, los triángulos PCS, SBR y RAQ también resultan equiláteros.

 

a) Como los triángulos ARB, BSC, CPD y DQA son todos iguales (isósceles de ángulos 15º,15º y 150º con base AB=BC=CD=DA) y como PCS, SBR, RAQ, QDP son equiláteros entonces:

 

 AR=RQ=QA=BR=RS=SB=SC=CP=PS=DP=PQ=DQ

 

Luego RQ=RS=PS=PQ y como SPQ= 360º-DPC-CPS-QPD= 360º-150º-60º-60º=90º

Análogamente los ángulos PQR, QRS y RSP también son 90º. Entonces como el cuadrilátero PQRS tiene todos sus lados iguales y sus ángulos miden 90° es un cuadrado.

 

Sea M el punto medio de AB y N el punto medio de DC. Como APB es equilátero entonces PM es perpendicular a AB luego por Pitágoras sabemos que PB²= MB² +MP²

 

 

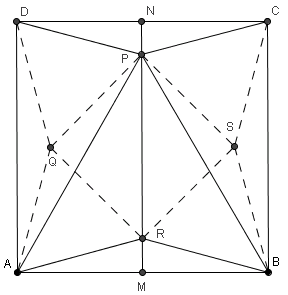
PB=AB=1

MB=1/2AB=0,5

1² = MP² + 0,5²

MP² =3/4

MP=

NP=1-MP=1-

Análogamente MR=1-

PR=PM-MR =

 

 

 

 

 

Como PQRS es un cuadrado, sus diagonales son iguales y QS= 1. Ahora vamos a usar que el área de un cuadrado es la mitad del producto de sus diagonales, luego:

 

(PQRS)= =

 

b) Si sólo conociéramos PQRS y quisiéramos obtener ABCD podríamos proceder de la siguiente manera. Para construir por ejemplo C basta con trazar el triángulo equilátero de base PS de forma que quede exterior al cuadrado PQRS pues ya hemos visto que el triángulo PSC debe ser equilátero.

 

Para construir un triángulo equilátero exterior a PQRS y de base PS procedemos de la siguiente manera:

 

• Se traza la circunferencia de centro S y radio SP
• Se traza la circunferencia de centro P y radio PS
• Se marca el punto C que es la intersección de las dos circunferencias antes trazadas exterior a PQRS (las dos circunferencias se intersectan en 2 puntos, uno interior a PQRS y otro exterior).

 

Verifiquemos que el punto que construimos, “C” verifica que PSC es un triangulo equilátero, para ello notemos que

 

• PS=PC ya que C pertenece a la circunferencia de centro P y radio PS
• SP=SC ya que C pertenece a la circunferencia de centro S y radio SP

 

Por lo tanto PS=PC=SC, es decir que PSC es equilátero.

 

Del mismo modo se trazan los triángulos equiláteros PQD, QRA y RSB y quedan determinados A, B, C, D. Por ultimo unimos A con B, B con C, C con D y D con A, y nos queda el cuadrado ABCD.