Problemas de Noviembre 2000

Los problemas no están separados por nivel. Traten de hacer todos, algunos les resultarán fáciles y otros difíciles. Cualquier cosa que no sepan o quieran preguntarnos no duden en escribirnos a mateclubes@oma.org.ar

También mandennos las soluciones de los problemas que resuelvan y no se olviden de contarnos cómo hicieron para resolverlos.

Mínimo Común Múltiplo

1

Betty arma una lista con los números naturales múltiplos de 7:
7, 14, 21, 28, ...

Rafa arma una lista con los números naturales múltiplos de 16:
16, 32, 48, ...

¿Cuál es el primer número que aparece en las dos listas?

2

Mario arma una lista con los números naturales múltiplos de 24:
24, 48, 72, 96, ...

Rafa arma una lista con los números naturales múltiplos de 15:
15, 30, 45, 60, ...

1. ¿Cuál es el primer número que aparece en las dos listas?
2. ¿Cuál es el siguiente número que aparece en las dos listas?

Betty arma una lista con todos los número que aparecen en las dos listas.

3. ¿Cuáles son los primeros 10 números de la lista de Betty?

El primer número que encontraron en los dos problemas se llama mínimo común múltiplo.

3

1. ¿Por cuánto hay que multiplicar a 2 . 3 . 7 para que resulte múltiplo de 3 . 5 . 7 . 7? (Buscá el número natural más chico posible.)
2. ¿Cuál es el mínimo común múltiplo entre 2 . 2 . 3 . 3 . 7 . 7  y  2 . 3 . 3 . 7 . 7 . 7 . 5?

4

Sebastián visita a su abuela Porota cada 5 días. El otro nieto de Porota, Matías, la visita cada 7 días. Cada vez que vienen, Porota tiene que levantarse temprano para ordenar la casa. Si el 1° de enero de 2001 van los dos a visitarla, ¿cuántas veces tendrá que levantarse temprano en ese año?

5 (este problema lo tomaron en el certamen nacional de la Olimpíada Matemática Ñandú de este año)

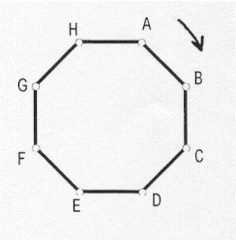
Una hormiga camina por el borde de un plato de 8 lados iguales como el de la figura.

Cada lado del plato mide 14 cm. La hormiga sale del vértice A y camina en el sentido que indica la flecha, siempre por el borde del plato. Hace la primer parada a 6 cm del vértice A y después, cada 6 cm hace una parado. En total hace 2000 paradas. ¿Cuántas veces para en el vértice A?

¿En qué otros vértices hace la misma cantidad de paradas que en A?

División y resto

1

1. ¿Cuánto hay que restarle a 100 para que resulte un múltiplo de 7?
2. ¿Cuál es el múltiplo de 13 más cercano a 200?

2

1. ¿Cuál es el resto en la división por 10 de 12345?
2. ¿Cuál es el resto en la división por 100 de 1823482752337?

3

1. ¿Cuál es el resto en la división por 9 de 5328?
   (recordá la regla de divisibilidad por 9)
2. ¿Cuál es el resto en la división por 9 de 1234?
3. ¿Cuál es el resto en la división por 9 de 1 + 2 + 3 + 4?
   Elegí otros números y fijate si cumplen la misma propiedad.

4

Andrés va a encontrarse con su novia el sábado a las 10 de la noche. El llega puntual, pero espera a su novia mil horas.

1. ¿A qué hora llegó su novia?
2. ¿Qué día de la semana era cuándo llegó?

5 (este problema lo tomaron en el certamen nacional de la Olimpíada Matemática Ñandú de este año)

En la pantalla de la computadora se ve una marca A y un disco que puede girar sobre su centro, como en la figura. El disco es blanco y el punto del borde que coincide con la marca A es de color rojo.

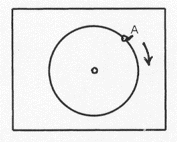Cada vez que se aprieta la tecla E, el disco gira 15' en el sentido de las agujas del reloj y, cuando se detiene, cambia el color del punto del borde del disco que coincide con la marca A, de la siguiente manera: si es blanco, cambia a rojo; si es rojo, cambio a azul; si es azul, cambia a rojo. Después de apretar la tecla E 2000 veces, ¿cuántos puntos rojos y cuántos puntos azules hay en el borde del disco?

¿Cuál es el menor número de veces que hay que apretar la tecla E para que haya más puntos ázules que rojos?