1
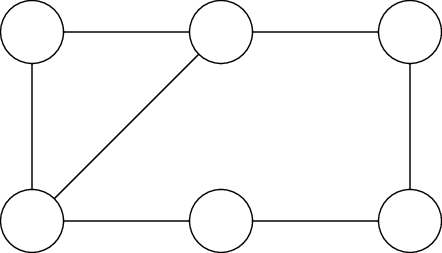
Rafa quiere pintar cada círculo de azul, rojo, negro o verde. Si dos círculos están unidos por un segmento no pueden estar pintados del mismo color.
¿De cuántas formas puede Rafa pintar los círculos?

Ingresar solución de este problema.
2
Mario quiere completar la figura colocando un número entero positivo en cada círculo y cuadrado, asegurándose de que todos los números sean distintos entre sí.
Además, a partir de la segunda columna, el número en cada círculo debe ser igual a la suma de los números desde los cuales salen flechas que llegan hacia él.
Por ejemplo, entre los números completados tenemos 135+234 = 369.
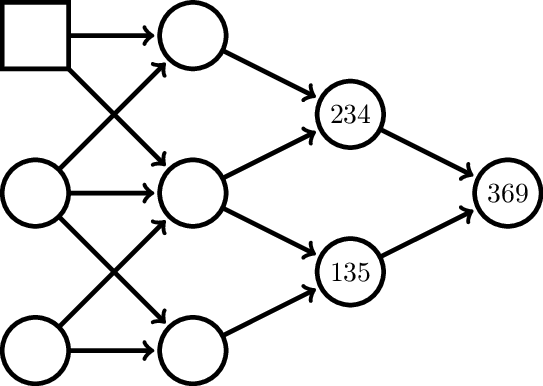
¿Cómo puede completar Mario la figura para que en el cuadrado quede el número más grande posible?
Ingresar solución de este problema.
3
Betty escribe en su cuaderno todos los números de 1 a 1000.
Luego, para cada número del cuaderno, escribe en el pizarrón los divisores de ese número. Es decir, escribe los divisores de 1, los divisores de 2, los divisores de 3, y así siguiendo hasta llegar a los divisores de 1000.
A Betty no le importa escribir el mismo número muchas veces. Por ejemplo, escribe el número 10 muchas veces (pues es divisor de varios números). De todos los números escritos en el pizarrón, ¿cuántos son múltiplos de 67?
Aclaración: Los divisores de un número N son aquellos números positivos d que hacen que N/d sea entero. Por ejemplo, los divisores del 385 son 1, 5, 7, 11, 35, 55, 77 y 385.
Ingresar solución de este problema.
Ver soluciones enviadas por tu club hasta el momento.
| Olimpíada Matemática Argentina www.oma.org.ar |
||
| mensajes mateclubes@oma.org.ar |