26ª Competencia de MateClubes 2023
Primera Ronda - Nivel 5

• La prueba dura 2 horas.
• Se puede usar calculadora. No se pueden consultar libros ni apuntes ni archivos de la computadora.
• No puede usarse ningún programa de la computadora para resolver los problemas.
• Los problemas deben ser resueltos por los alumnos participantes de cada club. No pueden consultar con otros clubes ni recibir ayuda de profesores o miembros adherentes (excepto en cuestiones informáticas relacionadas con la recepción y el envío de las pruebas).
• Las soluciones que nosotros recibamos deben haber sido escritas por los alumnos de cada club. Los profesores, bajo ninguna circunstancia, pueden escribir, tipear o transcribir las soluciones de los alumnos.

1

Mario dibujó en el pizarrón un tablero con 4 casillas.

Mario quiere completarlo con cuatro números enteros positivos, uno en cada casilla, de manera tal que el producto de los cuatro números sea 252. Quiere que la suma de los cuatro números que escribe sea lo más chica posible.

¿Cómo puede completar el tablero? ¿Cuánto suman las casillas? ¿Por qué es este el mínimo valor posible de la suma?

Ingresar solución de este problema.

2

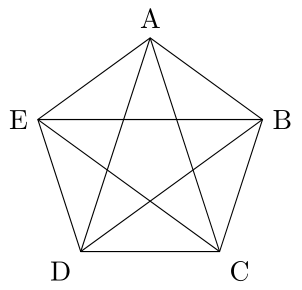
Un grillo salta entre los 5 vértices de un pentágono ABCDE. Comienza en el vértice A. Cada salto puede ser de un vértice, a cualquier otro. Al cabo de 6 saltos, el grillo terminó nuevamente en el vértice A.

¿Cuántos recorridos distintos pudo haber hecho el grillo? Explicar cómo los contaron.

Ingresar solución de este problema.

3

Betty sabe que entre sus 100 amigos, algunos siempre dicen la verdad, algunos siempre mienten, y otros a veces mienten y a veces dicen la verdad. Betty descubrió que aquellos amigos que a veces mienten y a veces dicen la verdad, lo hacen alternadamente: nunca dicen la verdad dos veces de manera consecutiva, ni mienten dos veces de manera consecutiva.

Betty quiere descubrir cuántos de sus amigos siempre dicen la verdad, cuántos de sus amigos siempre mienten, y cuántos alternan su respuesta. Para lograrlo, hace lo siguiente:

• Primero Betty dice ``Levanten la mano los que siempre dicen la verdad'' y 71 levantaron la mano.
• Luego Betty dice ``Levanten la mano los que a veces dicen la verdad y a veces mienten'' y 52 levantaron la mano.
• Finalmente, Betty dice ``Levanten la mano los que siempre mienten'' y 33 levantaron la mano.

Con esta información, ayuden a Betty a determinar cuántos amigos siempre dicen la verdad, cuántos siempre mienten, y cuántos alternan su respuesta.

Ingresar solución de este problema.

Ver soluciones enviadas por tu club hasta el momento.

Los MateClubes Competencias	Olimpíada Matemática Argentina    www.oma.org.ar
mensajes mateclubes@oma.org.ar