26ª Competencia de MateClubes 2023
Primera Ronda - Nivel 3

• La prueba dura 2 horas.
• Se puede usar calculadora. No se pueden consultar libros ni apuntes ni archivos de la computadora.
• No puede usarse ningún programa de la computadora para resolver los problemas.
• Los problemas deben ser resueltos por los alumnos participantes de cada club. No pueden consultar con otros clubes ni recibir ayuda de profesores o miembros adherentes (excepto en cuestiones informáticas relacionadas con la recepción y el envío de las pruebas).
• Las soluciones que nosotros recibamos deben haber sido escritas por los alumnos de cada club. Los profesores, bajo ninguna circunstancia, pueden escribir, tipear o transcribir las soluciones de los alumnos.

1

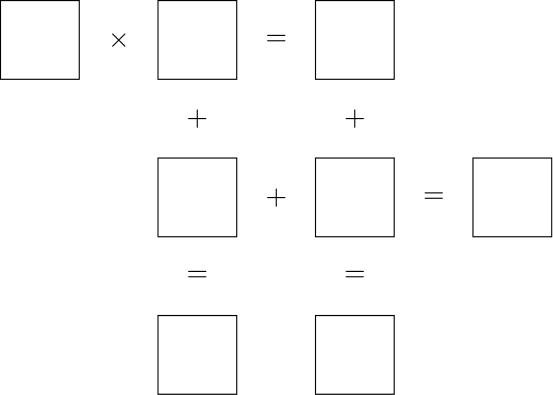
Rafa quiere completar los ocho cuadraditos con dígitos de 1 a 9, sin repetir (queda un dígito sin utilizar).

Quiere que las cuatro igualdades de la figura resulten correctas.

¿Cómo puede hacerlo?

Ingresar solución de este problema.

2

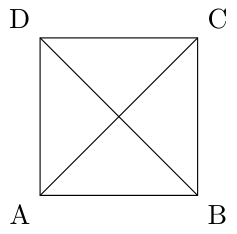
Un grillo salta entre los 4 vértices de un cuadrado ABCD. Comienza en el vértice A. Cada salto puede ser de un vértice a cualquier otro (no puede saltar al mismo vértice en el que está). Al cabo de 4 saltos, el grillo terminó nuevamente en el vértice A.

¿Cuántos recorridos distintos pudo haber hecho el grillo? Dar todas las posibilidades.

Ingresar solución de este problema.

3

Betty sabe que entre sus amigos, algunos siempre dicen la verdad, algunos siempre mienten, y otros a veces mienten y a veces dicen la verdad. Betty descubrió que aquellos amigos que a veces mienten y a veces dicen la verdad, lo hacen alternadamente: la primera vez mienten, la segunda vez dicen la verdad y la tercera vez mienten.

Betty quiere descubrir cuántos de sus amigos siempre dicen la verdad, cuántos de sus amigos siempre mienten, y cuántos alternan su respuesta. Para lograrlo, hace lo siguiente:

• Primero Betty dice "Levanten la mano los que a veces dicen la verdad y a veces mienten" y 41 levantaron la mano.
• Luego Betty dice "Levanten la mano los que siempre dicen la verdad" y 65 levantaron la mano.
• Finalmente, Betty dice "Levanten la mano los que siempre mienten" y 23 levantaron la mano.

Con esta información, ayuden a Betty a determinar cuántos amigos siempre dicen la verdad, cuántos siempre mienten, y cuántos alternan su respuesta.

Ingresar solución de este problema.

Ver soluciones enviadas por tu club hasta el momento.

Los MateClubes Competencias	Olimpíada Matemática Argentina    www.oma.org.ar
mensajes mateclubes@oma.org.ar