1
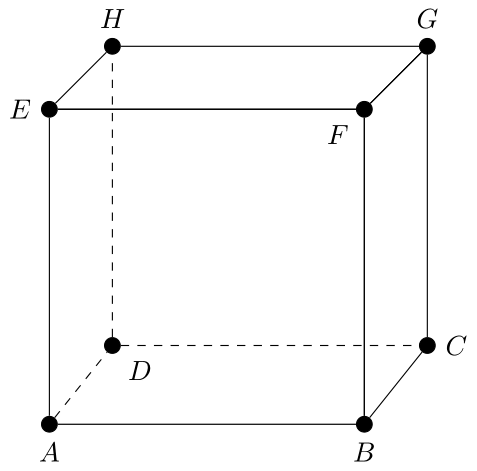
Betty tiene un cubo. Rafa escribe un 0 o un 1 en cada una de las aristas. Al finalizar, Betty se dio cuenta de que en cada una de las caras, la suma de las 4 aristas da 1.
¿De cuántas maneras distintas pudo Rafa haber escrito los números? Dar todas las posibilidades.
Ingresar solución de este problema.
2
Rafa dibuja en un círculo 20 puntos numerados en orden del 1 al 20. Betty, decide dibujar un segmento entre cada par de números que difieren en un número primo.
Por ejemplo, dibuja un segmento entre el 2 y el 13 porque difieren en 11.
Rafa quiere elegir 3 puntos de los 20 de forma tal que los 3 segmentos entre ellos hayan sido dibujados por Betty. Por ejemplo, puede elegir los puntos 1, 3 y 6.
¿De cuántas maneras puede hacerlo?
Aclaración: El 1 no es primo. Los números primos menores que 20 son: 2, 3, 5, 7, 11, 13, 17, 19.
Ingresar solución de este problema.
3
Mario quiere completar la figura usando los dígitos del 0 al 9 sin repetir, un dígito en cada casilla, de manera tal que los tres números de 4 cifras que se forman en las filas y columnas cumplan:
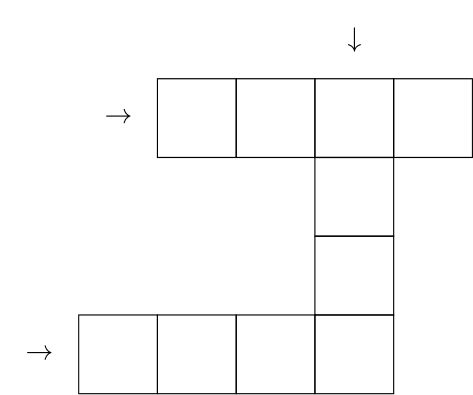
Si quiere que la suma de los tres números formados sea la mayor posible, ¿cómo debe completar la figura?
Ingresar solución de este problema.
Ver soluciones enviadas por tu club hasta el momento.
 Los
MateClubes Competencias |
Olimpíada Matemática Argentina www.oma.org.ar |
|
| mensajes mateclubes@oma.org.ar |