31 Instituto Científico Weizmann
Selección. Prueba de Matemática

10 de mayo de 1999

1. Hallar las soluciones de la ecuación:

3^2x + 3^x = 90

(10 puntos)

2. La víctima de un accidente morirá a menos que reciba en los próximos 10 minutos una transfusión de sangre tipo A-Rh positivo. Se dispone de gran número de donantes de los cuales sólo se sabe que el 40% tienen sangre de ese tipo. Se necesitan dos minutos para determinar el tipo de sangre del posible donante y dos minutos para realizar la transfusión. ¿Cuál es la probabilidad de que se salve si el hospital dispone de un sólo equipo de tipificación de sangre?

(10 puntos)

3. Sea a₁, a₂, a₃, a₄, a₅, a₆ una progresión geométrica de razón r. Si a₁ + a₂ + a₃ + a₄ + a₅ = 3124, y a₂ + a₃ + a₄ + a₅ + a₆ = 2343 , hallar r y a₃.

(10 puntos)

4. Para la construcción de una pista circular de patinaje sobre hielo, se tienen las propuestas de dos empresas. La empresa A cobra $40 por m2 de pista, $30 el metro de cerco y un adicional fijo de $400 para gastos generales. La empresa B cobra $36 por m2 de pista, $40 el metro de cerco y un adicional fíjo de $1200. ¿Para qué valores del diámetro de la pista es más ventajoso contratar la empresa A?

(12 puntos)

5. ¿Cuál es la probabilidad de las fechas de nacimiento de 4 personas tomadas al azar correspondan todas a dos meses cualesquiera del año quedando exactamente 10 meses libres? (Suponer que todos los meses son equiprobables.)

(12 puntos)

6. Sean ABC un triángulo y M el punto medio del lado BC. Si BC = a, AC = b, BAM = a, CAM = P y BMA = x, demostrar que

(14 puntos)

7. Sean x y d números naturales tales que el resto de dividir x por d es igual a 4 y el resto de dividir 14x por d es 17. Hallar el resto de dividir 210x por d.

(16 puntos)

8. ABCDEFGH es un cubo de arista l. Sean M el punto medio de AD y N el punto medio de DC. Calcular el área MEGN en fünción de l.

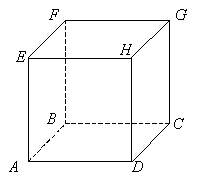
(16 puntos)

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar