I
Olimpíada Iberoamericana para
Estudiantes Universitarios
Ronda Preparatoria
14 de Mayo de 1998
1 (3 puntos)
Demostrar que el sistema de ecuaciones
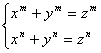
con m y n naturales diferentes no tiene soluciones en los números enteros positivos.
2 (4 puntos)
Demostrar las siguientes desigualdades
3 (4 puntos)
Encontrar todas las funciones f: R --> R, tales que
(f(x) - f(y))2
|x-y|3
para todos los números reales x e y.
4 (5 puntos)
En el espacio euclideano n-dimensional considérese un cubo unitario con centro en el origen de coordenadas. Los planos coordenados dividen este cubo en 2n cubos iguales de lado 1/2. En cada uno de estos 2n cubos se inscribe una esfera n-dimensional. Otra esfera n-dimensional con centro en el origen y radio rn es tangente a todas estas esferas exteriormente. Encontrar
5 (6 puntos)
Sea f:[0,1] --> [0,1] una
función continua y diferenciable tal que f(0)=0 y f(1)=1.
Demostrar que existen a, b 
(0,1), con a
b,
tales que
f' (a) . f'(b) = 1
6 (6 puntos)
Una isla del Caribe tiene la forma de un círculo
de radio R. En la isla hay una ciudad en forma de
círculo de radio r y la distancia desde el centro de la
ciudad al centro de la isla es 
. Así, en la isla viven
citadinos, campesinos y pescadores de manera que la distancia de
la casa de un pescador al mar es menor que la distancia de su
casa a la ciudad y la distancia de la casa de un campesino a la
ciudad es menor que al mar. Supongamos que la densidad de la
población en la isla es constante. Demuestre que los campesinos
y citadinos conforman menos del 25% y más del 24% de la
población, y que los citadinos conforman menos del 3% de la
población de la isla
7 (7 puntos)
Sea f: R --> R una función definida de la siguiente manera
Demostrar que si k es un número natural
y no es un cuadrado perfecto, entonces f es
diferenciable en 
.
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |