Pretorneo Internacional de las Ciudades
Segundo Pretorneo 1998

4 de Junio de 1998

1

Ana, Bea y Ceci hacen listas de palabras que se pueden formar con un conjunto dado de letras. Las tres listas tienen diferente número de palabras: la lista más larga es la de Ana y la más corta es la de Ceci. Cada palabra escrita que aparece en sólo una lista otorga 2 puntos al que la escribió. Cada palabra que está en exactamente dos listas otorga 1 punto a cada una de las paritcipantes que la escribieron. Si una palabra está escrita en las tres listas, no otorga puntos. ¿Es posible que Ceci sea la que tiene el mayor puntaje total y Ana sea la que tiene el menor puntaje total?

3 Puntos

2

El rey visita exactamente una vez cada casilla del tablero de ajedrez (8x8), regresando finalmente a su posición inicial. Demostrar que en su recorrida ha hecho un número par de movidas en diagonal.

ACLARACIÓN: En cada movida el rey se desplaza desde la casilla en que está a cualquiera de las vecinas con la que tiene un lado o un vértice en común.

4 Puntos

3

Sean AB y CD segmentos uno en cada uno de los lados de un ángulo de vértice O, tales que A está entre O y B, y C está entre O y D. Sean M y N los puntos medios de AD y BC, respectivamente. La recta MN intersecta a AB en P y a CD en Q. Demostrar que OP/OQ = AB/CD.

4 Puntos

4

Se forman todos los números de 3 dígitos y para cada uno de estos números se multiplican sus tres dígitos. Luego se suman todos los productos obtenidos. ¿Cual es el resultado?

5 Puntos

1

Se forman todos los números de 4 dígitos y para cada uno de estos números se multiplican sus cuatro dígitos. Luego se suman todos los productos obtenidos. ¿Cual es el resultado?

3 Puntos

2

¿Cuál es el máximo número de colores que se pueden utilizar para pintar un tablero de ajedrez (8x8) de modo tal que cada casilla tenga por los menos dos de sus vecinas (con un lado o vértice en común) pintadas del mismo color?

3 Puntos

3

Sean A, B, C, D número positivos tales que el sistema de ecuaciones

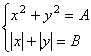
tiene m soluciones, mientras que el sistema de ecuaciones

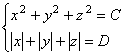
tiene n soluciones.
Si m > n > 1, hallar m y n.

5 Puntos

4

Una circunferencia de centro O está inscripta en un ángulo. Sea A el simétrico de O con respecto a uno de los lados del ángulo. Las tangentes a las circunferencias trazadas desde A intersectan al otro lado del ángulo en los puntos B y C. Demostrar que el circuncentro del triángulo ABC pertenece a la bisectriz del ángulo original.

ACLARACIÓN: El circuncentro de un triángulo es el centro de la circunferencia que pasa por los tres vértices del triángulo.

5 Puntos

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar