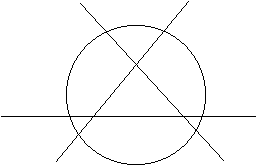
IV
Olimpíada Provincial
Buenos
Aires. 1996
Primer
nivel1. Tres rectas dividen a un círculo en 7 renglones (ver figura). ¿Es posible distribuir los números 1, 2, 3, 4, 5, 6, 7 uno en cada región de modo que para cada recta la suma de los números ubicados de un lado de la recta sea igual a la suma de los números ubicados del otro lado de la recta?
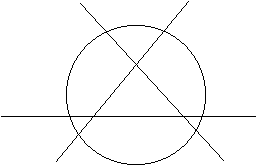
2. Sea ABCDE un pentágono que tiene AB=BC=4, CD=DE=EA=2 y CDE=DEA=120o. Hallar el área del pentágono.
3. Sea N un número de 3 dígitos
distintos. Con los dígitos de N se forman todos
los posibles números de 2 dígitos distintos; luego se
suman todos estos números de 2 dígitos y el resultado
es S.
Hallar todos los N tales que S es el
doble de N.
Segundo
nivel1.
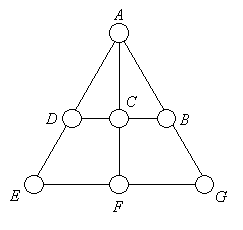
Hay que distribuir los números 1, 2, 3,
4, 5, 6, 7 uno en cada círculo del diagrama de modo que
la suma de los 3 números ubicados en tres círculos
alineados sea siempre la misma.
¿Qué número es imposible ubicar en el círculo E?
ACLARACIÓN: Los círculos alineados son: ABG, ACF, ADE, DCB, EFG.
2. Sean ABCD un cuadrado, E el punto medio del lado AB, F el punto medio del lado BC y Q el punto de intersección de EC y DF. Si QF=13, hallar las medidas de QC, QE y QD.
3. Hallar el menor múltiplo de 999, mayor que 999, que tiene todos sus dígitos impares.
Tercer
nivel1. Hallar todos los números enteros n de 5 dígitos tales que al suprimir el dígito del medio queda un número m de 4 dígitos que verifica que n/m es entero.
2. Por un punto P exterior a una
circunferencia C se trazan las
dos rectas tangentes; sean Q y R los
puntos de tangencia. Sea A un punto en la
prolongación de PQ y sea C'
la circunferencia circunscripta al triángulo PAR.
La recta AR corta a la circunferencia C
en R y en C.
Las circunferencias C y C'
se cortan en B y en R.
Demostrar que los ángulos PAR y ABC
son iguales.
3. Sea A un conjunto de números enteros entre
100 y 1000 inclusive, tal que sus elementos están en
progresión geométrica de razón mayor que 1. ¿Cuál es
la máxima cantidad de elementos que puede tener A?
ACLARACIÓN: La razón de la progresión geométrica
puede no ser un número entero, por ejemplo, 81, 108,
144, 192, 256 es una progresión geométrica de números
enteros y razón 4/3.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |