Primer nivel

1. La Asociación Vida Silvestre de Saladillo tiene 50 miembros. El sábado cada uno de los presentes plantó 17 árboles y el domingo cada uno de los presentes plantó 20 árboles. En total se plantaron 1545 árboles. ¿Cuántos de los miembros de la Asociación faltaron el sábado y cuántos faltaron el domingo?

2. Matías ha dibujado un cuadrado ABCD con tinta negra y debe colorear con rojo todos los puntos P del interior del cuadrado tales que el área del cuadrilátero BCPA es igual al triple del área del cuadrilátero APCD. Describir cuál es la parte roja del dibujo y justificar.

3. Se considera un polígono regular de 10 lados. Hay que elegir tres vértices de este polígono de modo tal que el triángulo que determinan sea escaleno y ningún lado del triángulo sea al mismo tiempo lado del polígono de 10 lados. ¿De cuántas maneras distintas se pueden elegir los tres vértices?

Segundo nivel

1. La computadora de Juan tiene un programa tal que al apretar la tecla S reemplaza al número N escrito en la pantalla por la suma de las cifras del número igual a N más la suma de las cifras de N. Por ejemplo, si el número de la pantalla es 9523, calcula 9+5+2+3+9523=9542, luego suma las cifras del resultado, 9+5+4+2=20, y el nuevo número que aparece en pantalla es 20.
Inicialmente el número escrito en pantalla es 1. ¿Qué número se tendrá en la pantalla después de apretar 1997 veces la tecla S.

2. Si la mediana y la altura correspondientes a un mismo vértice de un triángulo dividen al ángulo en tres ángulos iguales, hallar los ángulos del triángulo.

3. En cada casilla de un tablero cuadrado de 11x11 casillas se ha escrito un número mayor o igual que -1 y menor o igual que 1 (no necesariamente entero) de modo tal que la suma de los cuatro números ubicados en cada cuadrado de 2x2 sea siempre igual a 0. Hallar el máximo valor posible de la suma de los 121 números escritos en el tablero.

Tercer nivel

1. Hallar todos los enteros n tales que n+19 y n+97 son ambos potencias de 3.

2. Sea ABCD un rectángulo inscrito en una circunferencia. Sea P un punto en el arco AB de la circunferencia. La paralela a AB que pasa por P intersecta a las prolongaciones de DA y CB en P1 y P2 respectivamente. La paralela a BC que pasa por P intersecta a AB y CD en P3 y P4 respectivamente. Demostrar que P3 es el punto de intersección de las alturas del triángulo P1P2P4.

3. Una hormiga camina por las líneas de un tablero como el de la figura, con 4 casillas de ancho y 5 casillas de alto. ¿De cuántas diferentes maneras puede ir desde A hasta B, sin pasar dos veces por un mismo punto?

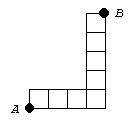Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar