Olimpíada Provincial de Buenos Aires 2001
Olimpíada Provincial de Córdoba 2001
Olimpíada Provincial de Santa Fe 2001
Olimpíada Metropolitana 2001

Primer Nivel

1

Un marciano tiene 321 pesos en monedas de 1 peso, de 5 pesos y de 25 pesos. Si tiene igual cantidad de monedas de 1 peso que de 5 pesos, determinar cuántas monedas de cada clase puede tener. Dar todas las posibilidades.

2

De un rectángulo PQRS se ha recortado un rombo ABCD de diagonales AC=8 y BD=6. Hallar el mínimo valor posible del área del rectángulo PQRS.

3

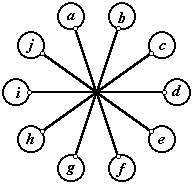
En el diagrama hay que reemplazar cada letra por uno de los números 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10. Un reemplazo de las diez letras es válido si a letras distintas le corresponden números distintos y además se verifican las siguientes cinco condiciones:

a + b = f + g

b + c = g + h

c + d = h + i

d + e = i + j

e + f = j + a

Determinar cuál es la cantidad de reemplazos válidos que tienen a = 1.

Segundo Nivel

1

Entre los números naturales de cinco cifras, determinar cuántos son pares y tales que el último dígito de la derecha (el de las unidades) es igual a la suma de los cuatro primeros dígitos.

2

Hallar el mayor entero positivo n para el que n! se puede expresar como producto de n - 3 enteros positivos consecutivos.

ACLARACIÓN: n! denota el producto de los primeros n enteros positivos, es decir, n! = 1 . 2 . 3 . ... . n. Por ejemplo, 5! = 1 . 2 . 3 . 4 . 5 = 120.

3

En una semicircunferencia de diámetro AD=3 se marcan los puntos B y C tales que los segmentos AB y BC son iguales, con AB=BC=1. Hallar la medida del segmento CD.

Tercer Nivel

1

Hallar todos los números enteros n tales que (n² + 7) / (n + 3) es también un número entero.

2

Sea n la suma de todas las potencias de 19, desde 19 hasta 19²⁰⁰¹:

n = 19 + 19² + 19³ + ... + 19²⁰⁰¹

Hallar el resto de la división de n por 7620.

3

Sean ABCD un rectángulo, M el punto medio del lado BC y P, Q puntos del lado AB tales que <AMQ = <QMP = <PMB y AQ = 2 BP. Calcular la medida del ángulo <AMB.

Nota: <AMB significa "el ángulo AMB"

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar