Cada problema vale 7 puntos.

1. Dado

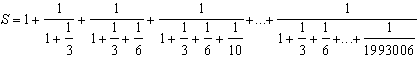
Donde el denominador está formado por las sumas parciales de la sucesión de los recíprocos de los números triangulares, demostrar que S > 1001.

2. Hallar un entero n, con 100 n 1997, tal que sea también entero.

3. Sean ABC un triángulo inscrito en una circunferencia, m_a, m_b, m_c las longitudes de las bisectrices del triángulo y , M_a, M_b, M_c las longitudes de las prolongaciones de dichas bisectrices hasta su segunda intersección con la circunferencia. Si

4. El tri&aautengulo A₁A₂A₃ es rectángulo en A₃. Se define una sucesión de puntos mediante el siguiente proceso iterativo para cada entero positivo n. Se traza desde A_n (n 3) la perpendicular al segmento A_n-2A_n-1 que lo intersecta en A_n+1.

a) Demostrar que si este proceso se continúa indefinidamente, entonces hay solamente un punto P en el interior de todos los triángulos A_n-2A_n-1A_n, n 3.

b) A₁ y A₃ puntos fijos. Hallar el lugar geométrico de los puntos P al variar A₂ en todas sus posibles ubicaciones.

5. Supongamos que n personas A₁, A₂, ... , A_n (n 3) están sentadas en círculo y que A_i tiene a_i objetos tales que a₁ + a₂ + ... + a_n = nN, donde N es un número positivo. Para que todas las personas tengan la misma cantidad de objetos, cada persona A₁ le da o recibe objetos de sus dos vecinos A_i-1 y A_i+1 donde A_n+1 quiere decir A₁ y A₀ quiere decir A_n. ¿Cómo se debe realizar esta distrbución para que el número total de objetos transferidos sea el mínimo?

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar