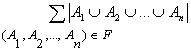
X Olimpíada de la Cuenca del Pacífico

12 de Marzo de 1998

1

Sea F el conjunto de todas las n-uplas (A₁,A₂,...,A_n) donde cada A_i, i=1,2,...,n es un subconjunto de {1,2,...,1998}. Denotamos con |A| al número de elementos del conjunto A. Hallar el número

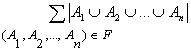
2

Demostrar que cualesquiera sean los números enteros positivos a y b, el producto (36a+b)(a+36b) no puede ser una potencia de 2.

3

Sean a, b, c números reales positivos. Demostrar que

.

4

Sea ABC un triángulo y D el pie de la altura dese A. Consideramos dos puntos E y F, ambos distintos de D y pertenecientes a una misma recta por D, tales que AE es perpendicular a BE y AF es perpendicular a CF. Sean M y N los puntos medios de BC y EF, respectivamente. Demostrar que AN es perpendicular a NM.

5

Determinar el mayor entero n con la propiedad de que n es divisible por todos los enteros positivos que son menores que .

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar