. Calcule las áreas de
las cuatro regiones en que los segmentos NC y MB dividen al
paralelogramo.VI Certamen el
Número de Oro
Profesores
de enseñanza media.
5 de Septiembre de 1998
1
Todos los vértices de una grilla cuadriculada de 6 x 2 se colorean de rojo ó de azul. Demuestre que queda determinado algún rectángulo con todos sus vértices del mismo color.
2
Sea n un número natural y sean p1, p2, ..., pn los primeros n números primos. Demuestre que p1p2.....pn + 1 no es un cubo perfecto.
3
En los lados AD y CD del paralelogramo ABCD de área 1 se
determinan puntos N y M, respectivamente, de manera que . Calcule las áreas de
las cuatro regiones en que los segmentos NC y MB dividen al
paralelogramo.
4
Caracterice todos los números reales b>1 tales que [logbx]
= [logb[x]] para todo número real x
1 (Aclaración: [ ] denota parte entera).
5
Determine todas las funciones continuas f : [0,1]
IR
tales que f(0) = f(1) = 0 y ![f((x+y)/2) <= f(x) + f(y) para todos x,y pertenecientes a [0,1]](oro98_2.gif){kind=small}
.
6
Dos remeros se entrenan cruzando repetidamente un río, con direcciones perpendiculares a las orillas y ambos con velocidades constantes. Al comenzar parten de orillas opuestas, y se cruzan en un punto situado a 31 metros de la orilla A. Cuando ambos han cruzado el río, retornan inmediatamente, y se cruzan esta vez a 18 metros de la orilla B. Determine el ancho del río.
7
Sean dados cuatro puntos del plano. Analice en qué casos existe una circunferencia que equidista de los cuatro.
8
¿Qué términos de la sucesión 0, 1, 1, 3, 5, 11, 21, ... son divisibles por 9 ?
9
Dos jugadores A y B practican el siguiente juego con dados: A arroja cinco dados y retiene para sí todos aquellos que registren un 6. Luego B arroja los restantes y realiza la misma operación, luego A hace lo mismo con los que queden, y así alternativamente, hasta que ya no queden dados. Se declara entonces ganador al jugador que posea la mayor cantidad de dados. Calcule la probabilidad de que gane A.
10
¿Cuál es el mínimo número de círculos de radio 1
necesarios para cubrir un círculo cuyo radio es el número de
oro 
? 
.
V Certamen el
Número de Oro. 1998
Estudiantes
de Profesorado y Licenciatura
5 de Septiembre de 1998
1
Calcule las raíces del polinomio x4 + 3x3 - 3x + 1, sabiendo que el producto de dos de ellas es -1.
2
Sean m y n números naturales tales que 
. Pruebe que 
.
3
Al arrojar 12 veces un dado, cada número apareció exactamente dos veces. ¿Es posible que los unos hayan aparecido consecutivamente, el segundo 2 dos tiros después del primer 2, el segundo 3 tres tiros después del primer 3, etc., etc.?
4
Sea f : IR IR una función no decreciente tal que f(x+1)
= f(x) + 1 
x.
Si f(0) es entero, demuestre que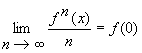 
. (Aclaración: f
n denota la composición f o f ... o
f , n veces).
5
Con tres segmentos que parten del centro de un cuadrado, ¿es posible dividir a éste en tres regiones que tengan la misma área y el mismo perímetro?
6
¿Cuántas potencias de 2 menores o iguales que 21000 tienen por primer dígito a 1?
7
Los vértices de un polígono convexo con un número impar de lados se colorean de azul, rojo ó verde, de manera que dos vértices adyacentes cualesquiera tienen diferente color. Pruebe que usando diagonales, el polígono puede descomponerse en triángulos de forma tal que los vértices de cualquier triángulo resulten de diferentes colores.
8
Consideremos la sucesión definida recursivamente por: a0 =
1
y ![a_n = a_(n-1) + [raíz de a_(n-1)] (n>0)](oro98_6.gif){kind=small}
. Demuestre que
infinitos términos de la sucesión son cuadrados perfectos.
(Aclaración: [ ] denota parte entera).
9
Dos jugadores A y B practican el siguiente juego con dados: A arroja cinco dados y retiene para sí todos aquellos que registren un 6. Luego B arroja los restantes y realiza la misma operación, luego A hace lo mismo con los que queden, y así alternativamente, hasta que ya no queden dados. Se declara entonces ganador al jugador que posea la mayor cantidad de dados. Calcule la probabilidad de que gane A.
10
¿Cuál es el mínimo número de círculos de radio 1
necesarios para cubrir un círculo cuyo radio es el número de
oro ? .
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |