de grado
con coeficientes enteros tiene al menos una raíz entera. Pruebe que P(0) ó
P(1) es par.XIII Certamen el
Número de Oro. 2005
Profesores
de enseñanza media.
1 Si m, n y p son primos mayores que 3 que forman una progresión aritmética de razón r, pruebe que 6 divide a r.
2 Indique cómo construir con regla y compás el cuadrilátero ABCD del que se conoce la longitud de los cuatro lados y el segmento que une los puntos medios de los lados opuestos DA y BC.
3 El
polinomio
de grado
con coeficientes enteros tiene al menos una raíz entera. Pruebe que P(0) ó
P(1) es par.
4 ¿Cuál es el menor n tal que al lanzar n veces 2 dados equilibrados, la probabilidad de que salga un doble 6 es mayor que la del suceso contrario?
5 Dados 7 puntos en un círculo de radio r tales que la distancia entre dos cualesquiera de ellos es mayor o igual que r. ¿Cuáles son las posibles distribuciones de los puntos?
6 Sea P un paralelepípedo rectángulo de lados a, b y c de longitudes números naturales tales que c mide igual a la diagonal del rectángulo de lados a y b. Pruebe que el volumen de P es múltiplo de 60.
7
Pruebe que la hipérbola de
tiene infinitos puntos de
coordenadas enteras.
8 Halle
todos los primos p para los cuales el
período primitivo del desarrollo decimal de
tiene longitud 6.
9
Sea la función f definida para los pares de enteros no negativos
por
y
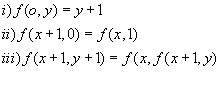
.10
ABCDE
es una pirámide recta de base un cuadrado de lado a y de altura h. ¿Cuál
es la relación
para que el área lateral de la pirámide
( la suma de las áreas de las cuatro caras triangulares) sea igual al área
lateral del cubo de lado h?
XII Certamen el
Número de Oro. 2005
Alumnos
del Profesorado
1 Pruebe
que si a es un número natural,
, entonces
es irracional.
2 Dado el paralelogramo ABCD de área 1 y los puntos medios E, F, G y H de sus lados, calcule el área del octógono cuyos vértices están determinados por las intersecciones de los segmentos que unen cada punto medio con los extremos del lado opuesto del paralelogramo.
3 Los ingenieros de una fábrica de robótica y aprovechando que ésta se encuentra sobre un camino rectilíneo, planificaron el siguiente experimento. A partir del mojón 0, dispusieron mojones numerados situados a 0,5m de distancia entre dos consecutivos. A partir del mojón 10235 un robot avanza 3 mojones y retrocede 8. En el paso siguiente avanza 6 mojones y retrocede 16. Reitera el procedimiento de duplicar el avance y el retroceso en cada paso. Al cabo de n pasos volvió al mojón 0. ¿Cuántos metros caminó el robot?
4 ¿Cuál es el menor n tal que al lanzar n veces 2 dados equilibrados, la probabilidad de que salga un doble 6 es mayor que la del suceso contrario?
5
¿Es
el número real
un número entero?
6 ¿Cuál es el máximo del subconjunto de números
reales
? ( N es el conjunto de números naturales).
7 Analice
el número de soluciones reales del siguiente sistema de ecuaciones, donde a es
un número real:
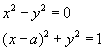
8 El triángulo ABC es rectángulo en A y BPQC, ACDE y ANMB son cuadrados construidos sobre los lados BC, CA y AB respectivamente y hacia el exterior del triángulo. El segmento AH , H perteneciente al lado PQ, es perpendicular a la hipotenusa BC. Pruebe que los segmentos CM, AH y BD se cortan en un punto situado en el interior del triángulo.
9
Sea
la función f definida para los pares
de enteros no negativos
por
y
.
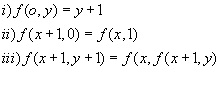
10
ABCDE
es una pirámide recta de base un cuadrado de lado a y de altura h. ¿Cuál
es la relación
para que el área lateral de la pirámide
( la suma de las áreas de las cuatro caras triangulares) sea igual al área
lateral del cubo de lado h?
 Archivo de
Enunciados Página
Principal  Soluciones |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |