XI Certamen el Número de Oro. 2003
Profesores de enseñanza media.

1  Sea ABC un triángulo equilátero de lado 1. Por una paralela al lado BC se divide al triángulo en dos figuras de igual área. Calcule la distancia entre ambas paralelas.

2  Determine el número de soluciones reales de la ecuación .

3  Un mago asegura a su interlocutor que puede conocer el día y mes de su nacimiento si él le da un sólo número. Debe multiplicar el día por 12 y el número del mes por 31 y darle el valor de la suma  de ambos productos. El interlocutor da al mago el número 574. ¿Cuál fue la respuesta de éste?

4  ¿De cuántas maneras pueden pintarse las 8 casillas del esquema de abajo si se dispone de 11 colores y bajo la condición de que si dos casillas tienen un lado en común entonces deben pintarse de distinto color?

5  Halle los cinco mayores números de cinco cifras y múltiplos de 11 que pueden formarse con los dígitos 2,3,4,5 y 6, pudiendo repetirse éstos.

6  Sea m un número natural con la propiedad de que todo subconjunto de m elementos del conjunto  contiene alguna progresión aritmética de 5 términos. ¿Cuál es el menor valor posible de m?

7 Consideremos en R² un sistema ortogonal de coordenadas ( O,X,Y,Z). Sean A y B dos puntos fijos  ( diferentes del origen) situados en los ejes OX y OY respectivamente y sea C un punto variable del eje OZ. Halle el lugar geométrico que determinan los baricentros de los triángulos ABC cuando C recorre el eje OZ.

8 Encuentre un polinomio  P(x) tal que P(x)  sea  divisible por   x² +1   y   P(x) +1  lo sea por  x³ + x² +1.

9 Determine el volumen de un tetraedro regular sabiendo que el área de la sección del mismo determinada por un plano perpendicular a la base que pasa por una arista lateral del tetraedro es .

10   Considere la cruz de Lorena formada por 13 cuadrados  de lado 1 como  indica la  figura. Determine el  punto  Q en  el segmento  AB tal que  la recta  PQ  divida a la  cruz en dos  superficies de  igual área.

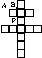
X Certamen el Número de Oro. 2003
Alumnos del Profesorado

1     En los lados del cuadrilátero ABCD se marcan los puntos E, F, G y H, cuyas distancias  a los vértices A, B, C y D son respectivamente, un tercio de los lados AB, BC, CD y DA.
Halle la relación entre las áreas de los cuadriláteros  EFGH y ABCD.

2  Determine los números naturales menores que 1000 que son capicúas escritos tanto en base 9 como en base 10.

3  Trazando segmentos desde el centro a cada uno de los vértices, se divide un hexágono regular en 6 triángulos. Se desea pintar cada uno de ellos de un color elegido entre blanco, negro, amarillo y  rojo, con la condición de que sectores vecinos se pinten de distinto color. ¿De cuántas maneras puede hacerse?.

4  Sean    funciones continuas tales que su composición verifica . Si  f es  creciente,  demuestre que f y g tienen un punto fijo en común.

5 Sea ABC un triángulo y sea PMN un triángulo inscripto en él de modo que los puntos P,M y N pertenecen respectivamente a los lados AB, BC y CA. Inscriba en PMN un triángulo semejante a ABC.

6 ¿Para qué valores de n resultan coprimos   1+2+….+n     y     12 + 22 +…..+ n2 ?

7 Consideremos en R² un sistema ortogonal de coordenadas ( O,X,Y,Z). Sean A y B dos puntos fijos  (diferentes del origen) situados en los ejes OX y OY respectivamente y sea C un punto variable del eje OZ. Halle el lugar geométrico que determinan los baricentros de los triángulos ABC cuando C recorre el eje OZ.

8 Encuentre un polinomio P(x) tal que P(x) sea divisible por x2 +1 y P(x) +1 lo sea por x3 + x2 +1.

9  Un tetraedro regular ABCD de arista b se divide en dos cuerpos de igual volumen por un plano  paralelo al plano  determinado por los vértices A. B y C. Halle la distancia entre los planos  y .

10 Considere la cruz de Lorena formada por 13 cuadrados  de lado 1 como  indica la  figura.Determine el  punto  Q en  el segmento  AB tal que  la recta  PQ  divida a la  cruz en dos superficies de  igual área.

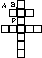
Archivo de Enunciados Página Principal Soluciones	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar