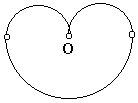
VIII Certamen
el Número de Oro
Profesores
de enseñanza media.
9 de Septiembre de 2000
1
Si a es un número real positivo (a <> 1), ¿cuántas soluciones tiene la ecuación loga x = x?
("a <> 1" significa "a distinto de 1")
2
La siguiente figura está formada por 3 semicírculos. Entre las rectas que pasan por O, ¿cuántas dividen su perímetro en dos partes iguales? ¿cuántas dividen el área en dos partes iguales?
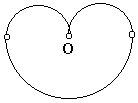
3
Sean a, b, c y d números reales positivos tales que a <> b ó c <> d. Pruebe que a / b + bd / ac + c / d > 3 .
4
Sea a un número real mayor que 1/8 . Calcule
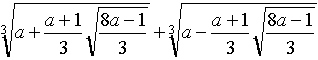 .
.
5
Un deportista se entrenará al menos una hora por día durante 7 semanas, a lo sumo 11 horas por semana. Demuestre que habrá un período de días consecutivos en los que en total se entrenará exactamente 20 horas
(Aclaración: cada día se entrena un número entero de horas).
6
Determine todas las permutaciones a1a2a3...a9a10 del conjunto {1, 2, 3, ... , 10} tales que el número determinado por a1a2a3...ak sea múltiplo de k para todo k entre 1 y 10 .
7
¿Cuál es el área mínima que puede tener un cuadrado en el plano que tenga en su interior exactamente 3 puntos de coordenadas enteras ?
8
Si n es un número natural, consideremos los números combinatorios
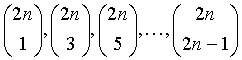
¿Cuál es el máximo común divisor de todos ellos ?
9
Se considera al azar una matriz de 6x6 cuyos elementos son 0 ó 1.¿Cuál es la probabilidad de que su determinante sea impar?
10
Pruebe que la serie
0.1 + 0.01 + 0.002 + 0.0003 + 0.00005 + 0.000008 + 0.0000013 + ...
converge y calcule su suma.
VII Certamen el
Número de Oro. 2000
Estudiantes
de Profesorado y Licenciatura
9 de Septiembre de 2000
1
¿Existe una función continua f : R --> R tal que f (f (x)) = - x para todo x real.
2
En un tetraedro regular de lado 8 cm se dan los puntos P y Q situados en las alturas correspondientes al lado común de las caras ABC y DBC, a un 1cm y 3 cm de los vértices A y D respectivamente.Un insecto camina por las caras del tetraedro desde P a Q. ¿Cuál es el trayecto de longitud mínima que puede recorrer?
3
Sea A un conjunto de 10 números naturales menores que 100. Pruebe que A contiene dos subconjuntos no vacíos, disjuntos entre sí, tales que la suma de los elementos de cada uno de ellos es la misma.
4
Si se escriben los números naturales de 1 a 1.000.000, ¿ cuál es la suma de todos los dígitos escritos ?
5
Se generan secuencias de números de dos dígitos en la siguiente forma: se elige uno cualquiera entre 00 y 99, se invierten sus cifras y luego se le suma la suma de las cifras (si el número obtenido supera a 99 se toma su resto de dividirlo por 100). Luego se repite sucesivamente el proceso hasta que un número se repita. Por ejemplo, la secuencia 58, 98, 06, 66, 78, .... ¿ Cuál es el máximo número de términos que puede tener una secuencia ?
6
Halle todos los pares (m, n) de números naturales tales que
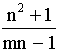
es un número entero.
7
Dado en el plano un triángulo de área 1, cuyos lados están cubiertos por 3 rectángulos de lados paralelos a los ejes coordenados, demostrar que la suma de las áreas de los rectángulos es mayor o igual que 1.
8
Determine los polinomios f de grado 2 con coeficientes enteros tales que f (m) es un cuadrado perfecto para todo m entero.
9
Se considera al azar una matriz de 6x6 cuyos elementos son 0 ó 1. ¿Cuál es la probabilidad de que su determinante sea impar?
10
Pruebe que la serie
0.1 + 0.01 + 0.002 + 0.0003 + 0.00005 + 0.000008 + 0.0000013 + ...
converge y calcule su suma.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |