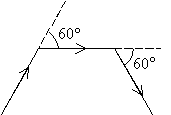
VI
Olimpíada Matemática RioplatenseMendoza, 10 y 11 de
diciembre de 1997
Nivel
APrimer
día
1
Hay 1997 números escritos alrededor de una circunferencia: 1996 son 0 y uno de ellos es 1. La única operación permitida es elegir un número y modificar sus dos vecinos, reemplazando 0 por 1 y 1 por 0.
2
Demostrar que no es posible dibujar dos triángulos de área 1 dentro de un círculo de radio 1 de manera que los triángulos no tengan puntos en común.
3
Al concierto del Instituto Rioplatense de la Matemática asistieron 1997 personas entre peruanos, bolivianos, paraguayos y venezolanos. Cada persona pagó su boleto de entrada la cantidad entera comprendida entre $1 y $499, inclusive, que voluntariamente quiso aportar.
Segundo día
4
Un tablero cuadrado de 4x4 está dividido en cuadraditos de 1x1. Hay un número secreto escrito en cada cuadradito de 1x1. Sólo se sabe que la suma de los cuatro números de cada fila es igual a 1, la suma de los cuatro números de cada columna es igual a 1 y la suma de los cuatro números de cada diagonal es igual a 1. ¿Es posible, con esta información, determinar la suma de los cuatro números de las esquinas y la suma de los cuatro números de los cuatro cuadraditos centrales? Si la respuesta es afirmativa, determinar la suma, si es negativa, explicar por qué.
5
¿Cuál es el menor múltiplo de 99, cuyos dígitos suman 99 y que empieza y termina con 97?
6
Un turista, de visita en Mendoza, decide hacer un paseo por la ciudad. El paseo se realiza por etapas. Cada etapa consta de 3 segmentos, cada uno de ellos de longitud 100m, y dos giros de 60o a la derecha, como se muestra en la figura. Entre el último segmento de una etapa y el primero de la siguiente, se hace un giro a la izquierda de 60o. ¿A qué distancia estará el turista del punto inicial después de haber recorrido 1997 etapas?
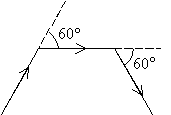
Nivel
1Primer
día
1
En un cuadrado ABCD de área 1, E es el punto medio de DC, G es el punto medio de AD, F es el punto del lado BC tal que 3CF=FB y O es el punto de intersección entre FG y AE. Encontrar el área del triángulo EFO.
2
Ignacio escribió un número entero mayor que cero. Usando exactamente los dígitos del número de Ignacio, pero en otro orden, Sofía escribió otro número que resultó ser igual a 1/3 del número de Ignacio.
3
Hay un triángulo T dibujado en una hoja de
papel blanco y se dispone de dos hojas de papel celeste.
En cada hoja de papel celeste está permitido dibujar un
solo triángulo, semejante a T (es decir con
ángulos iguales a los de T), pero de menor
tamaño, y luego recortarlo. ¿Es siempre posible obtener
dos triángulos de papel celeste (tal vez distintos entre
sí) y ubicarlos sobre la hoja blanca, de modo que el
triángulo T quede completamente tapado?
Justifique.
Aclaración: los triángulos celestes pueden superponerse
o no, y pueden sobresalir del triángulo dibujado o no.
Segundo día
4
Un número "divi" es aquel que es divisible por el número de divisores positivos que tiene. Por ejemplo, el 8 es divi porque tiene 4 divisores (1, 2, 4, 8) y el cuatro divide al 8. A los números divi que son cuadrados perfectos se los llama "dividivi". Hallar todos los números dividivi menores que 1997.
5
En un grupo de personas, se sabe que cada una de ellas conoce exactamente a 101 personas del grupo.
Aclaración: se supone que si A conoce a B, entonces B conoce a A.
6
Agustina y Santiago juegan al siguiente juego sobre una hoja rectangular:
Agustina dice un número natural n.
Santiago marca n puntos sobre la hoja.
Agustina elige algunos de los puntos marcados por Santiago.
Santiago gana el juego si logra dibujar un rectángulo de lados paralelos a los bordes de la hoja, que contenga todos los puntos elegidos por Agustina y no contenga ninguno de los puntos restantes. De lo contrario, Agustina gana el juego.
¿Cuál es el menor número que puede decir Agustina para asegurarse de poder ganar el juego independientemente de cómo haya dibujado Santiago los puntos? Justificar.
Nivel
2Primer
día
1
Sea n un entero, n![]() 2. Cada uno de los cuadros de un
tablero nxn
se colorea de blanco, amarillo o verde de acuerdo con los
siguientes criterios:
2. Cada uno de los cuadros de un
tablero nxn
se colorea de blanco, amarillo o verde de acuerdo con los
siguientes criterios:
- los cuadros en las posiciones (i, i) para 1
i
n se colorean de blanco;
- los cuadros en las posiciones (i, j) para i
j se colorean de amarillo o verde;
- para cualesquiera i, j, k tales que los cuadros en las posiciones (i, j) u (j, k) son del mismo color, el cuadro en la posición (i, k) también es de ese mismo color.
Aclaración: el cuadro en la posición (i, j) es el que está en la i-ésima fila y en la j-ésima columna.
2
Demostrar que existe un único conjunto no vacío S de enteros con las siguientes propiedades:
3
Sea ABCD un tetraedro regular, P y Q puntos distintos en los planos BCD y ACD respectivamente. Demostrar que existe un triángulo cuyos lados miden AP, PQ y QB.
Segundo día
4
Calcular la suma
![]()
5
Sea S un conjunto infinito de puntos del
plano con la siguiente propiedad: Si A, B,
C son puntos distintos de S, entonces
la distancia desde A hasta la recta BC
es un número entero.
Demostrar que todos los puntos de S están en
una misma recta.
6
Dada una sucesión infinita de dígitos a1,
a2, a3, ... , an,
... , se intercalan infinitos signos ![]() en la sucesión y para cada par
de signos
en la sucesión y para cada par
de signos ![]() consecutivos se
considera el número formado por los dígitos
comprendidos entre ambos signos
consecutivos se
considera el número formado por los dígitos
comprendidos entre ambos signos ![]() .
.
Aclaración: Puede haber términos de la sucesión a
la izquierda del primer signo ![]() . Éstos no están comprendidos
entre dos signos
. Éstos no están comprendidos
entre dos signos ![]() .
.
Nivel
3Primer
día
1
Hallar todos los enteros positivos n con la siguiente propiedad: existe un polinomio Pn(x) de grado n, con coeficientes enteros, tal que Pn(0)=0 y Pn(x)=n para n valores enteros y distintos de x.
2
Considerar un prisma, no necesariamente recto, cuya base es un rombo ABCD con lado AB=5 y diagonal AC=8. Una esfera de radio r es tangente al plano ABCD en C y tangente a las aristas AA1, BB1 y DD1 del prisma. Calcular r.
3
Demostrar que hay infinitos enteros positivos n tales que la cantidad de divisores positivos que tiene 2n-1 es mayor que n.
Segundo día
4
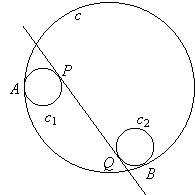
Las circunferencias c1 y c2 son tangentes interiormente a la circunferencia c en los puntos A y B, respectivamente, como se ve en la figura. La tangente interior común a c1 y c2 toca a estas circunferencias en P y Q, respectivamente. Demostrar que las rectas AP y BQ intersecan a la circunferencia c en puntos diametralmente opuestos.
5
Sean x1, x2,
... , xn números no
negativos n![]() 3 tales que
3 tales que
x1 + x2 + ... + xn = 1.
Determinar el máximo valor posible de la expresión x1x2 + x2x3 + ... + xn-1xn.
6
Sea N el conjunto de los números
enteros positivos.
Determinar si existe una función f: N-->N
tal que f(f(n))=2n,
para todo n![]() N.
N.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |