XVIII Olimpíada
Matemática Rioplatense
Diciembre de 2009
| Nivel A |
1. En
una caja hay 2009 bolitas numeradas del 1 al 2009, y fuera de la caja hay
bolitas sin numerar. Andrés repite el siguiente procedimiento hasta que quede
sólo una bolita en la caja.
Cada vez saca dos bolitas de la caja:
· * si los números de las bolitas son distintos, divide el mayor por el menor, y
o si el resto es cero, regresa a la caja la bolita con el menor número.
o si el resto es distinto de cero, numera una bolita con dicho resto y la coloca en la caja.
· * si los números de las bolitas son iguales, regresa una de las bolitas a la caja.
Determinar todos los posibles números que pueden aparecer en la bolita
que queda al final.
ACLARACIÓN:
El resto (residuo) en la división de 1055 por 13 es 2 porque 1055 = 13
x 81 + 2.
El resto en la división de 75 por 15 es 0 porque 75 = 15 x 5 + 0.
2. (a) De un cuadrado de papel de lado 10 se recortan rectángulos de 1 x 8, con cortes paralelos a los lados del cuadrado. Determinar cuál es la mayor cantidad de rectángulos de este tipo que se puede obtener.
(b) De un cuadrado de papel de lado 80 se recortan rectángulos de 1 x 43, con cortes paralelos a los lados del cuadrado. Determinar cuál es la mayor cantidad de rectángulos de este tipo que se puede obtener.
En ambos casos, indicar cómo se realizan los cortes y
explicar por qué no es posible recortar una cantidad mayor de rectángulos.
3. En el concurso del Monedado participan equipos formados por 75 niños y 25 niñas.
El organizador decide la ubicación de los cien integrantes del equipo en 100 sillas alrededor de una mesa circular y le da una moneda a cada uno. Cuando el organizador da la orden, cada integrante entrega su moneda a uno de sus dos vecinos o bien se queda con ella. Hecho esto, el organizador otorga al equipo un punto por cada niño que tenga exactamente una moneda, un punto por cada niña que tenga exactamente dos monedas y ningún punto por cada integrante que se encuentre en cualquier otra situación.
Determinar cuál es el puntaje máximo que puede obtener el equipo e indicar cómo deben organizarse los integrantes para obtener dicho puntaje máximo.
4. En un tablero de 2 x 13 Sofía escribe un número en cada una de las casillas de la primera fila. En cada casilla de la segunda fila Pablo escribe cuántos números de la primera fila son mayores que el que está en la casilla de arriba. Por ejemplo:
|
Sofía |
2 |
3 |
7 |
7 |
1 |
4 |
2 |
9 |
17 |
21 |
23 |
12 |
8 |
|
Pablo |
10 |
9 |
6 |
6 |
12 |
8 |
10 |
4 |
2 |
1 |
0 |
3 |
5 |
En las siguientes tablas se han borrado los números escritos por Sofía:
|
Sofía |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pablo |
7 |
7 |
11 |
3 |
0 |
1 |
9 |
10 |
5 |
5 |
6 |
2 |
4 |
|
Sofía |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pablo |
3 |
6 |
6 |
6 |
0 |
1 |
11 |
11 |
9 |
4 |
5 |
10 |
1 |
Determinar en cada caso si los números escritos por Pablo pueden corresponder a una lista escrita por Sofía. Si la respuesta es sí, dar una posible lista de Sofía, si la respuesta es no, explicar por qué.
5. En un tablero de 9 x 9 casillas blancas se colorean de negro algunas casillas de manera que se cumplan las tres condiciones siguientes:
· * Cada fila y cada columna tiene al menos una casilla coloreada de negro.
· * No hay dos filas con el mismo número de casillas coloreadas de negro.
· * No hay dos columnas con el mismo número de casillas coloreadas de negro.
Si en un tablero que cumple lo anterior se recorta un rectángulo de lados paralelos a los lados del tablero, formado únicamente por casillas blancas, ¿cuál es la mayor cantidad de casillas que puede tener dicho rectángulo?
6. Se tiene 10 pesas de igual aspecto y pesos distintos, iguales a 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10 gramos. Un empleado distribuye 10 etiquetas que dicen 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10 a las pesas indicando el peso correspondiente pero puede cometer errores. Mostrar que usando 3 veces una balanza de platos se puede determinar con certeza si el empleado cometió o no errores. (La balanza de platos indica si los objetos en cada plato pesan igual o cual pesa más y cual pesa menos)
| Nivel 1 |
1. ABC es un triángulo cuyos lados miden BC = 5, AC = 4 y AB = 3. Sean I el centro de la circunferencia tangente internamente a los tres lados del triángulo ABC (incírculo) y M el punto medio de BC. Las perpendiculares al lado AB que pasan por M y por I intersectan al lado AB en R y S, respectivamente. La recta MI corta al lado AB en el punto P. Demostrar que los segmentos RS y SP tienen la misma medida.
2. Decimos que un entero positivo N “cubre al 2009” si los dígitos 2, 0, 0, 9 aparecen en ese orden entre los dígitos de N. Por ejemplo, 1230089 cubre al 2009, pero 29091 no cubre al 2009.
(a) Demostrar que todo entero positivo se puede expresar de la forma A – B, donde A y B son enteros positivos tales que A cubre al 2009 y B no cubre al 2009.
(b) Demostrar que todo entero positivo se puede expresar de la forma C – D, donde C y D son enteros positivos que no cubren al 2009.
3.
¿De cuántas maneras se puede cubrir, sin superposiciones ni huecos, un tablero
de 5 x 5
con una ficha de la forma
![]() y
5 fichas de la forma
y
5 fichas de la forma
![]() ?
?
ACLARACIÓN: está permitido rotar y voltear las fichas.
Segundo Día
4. Determinar cuántos números de cuatro dígitos son múltiplos de 11 y tienen todos sus dígitos diferentes.
5.
En cada casilla de un tablero de 100 x
100 está escrito un signo +.
Una operación permitida consiste en elegir una fila o columna y cambiar
todos los signos de esa línea (los signos + por signos – y
viceversa).
Diremos que un número N es bueno si mediante una secuencia de
operaciones permitidas se puede lograr un tablero con exactamente N
signos –.
Determinar cuántos son los números buenos menores o iguales que 1000.
6.
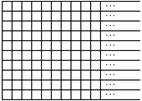 Determinar
si es posible distribuir todos los enteros positivos en las casillas de un
tablero de 10 filas e infinitas columnas como se muestra en la figura, de forma
tal que se cumplan las siguientes condiciones a la vez:
Determinar
si es posible distribuir todos los enteros positivos en las casillas de un
tablero de 10 filas e infinitas columnas como se muestra en la figura, de forma
tal que se cumplan las siguientes condiciones a la vez:
* Cada entero positivo aparece exactamente una vez en el tablero.
o * Si a, b, c son los números que aparecen de izquierda a derecha en tres casillas consecutivas de una misma fila, se cumple que a + b es un divisor de b + c.
| Nivel 2 |
1.
Sea X un punto interior del triángulo ABC, y
sea Y un punto interior del triángulo AXC tal que
![]() e
e
![]() Sea
P el simétrico de X respecto de la recta AB. Sea Q
el simétrico de X respecto de la recta BC. Demostrar que los
segmentos PY y QY son iguales.
Sea
P el simétrico de X respecto de la recta AB. Sea Q
el simétrico de X respecto de la recta BC. Demostrar que los
segmentos PY y QY son iguales.
2. Se tienen 2009 sucesiones finitas de 0 y 1. Ninguna de ellas coincide con el comienzo de otra. Si n es el total de 0 y 1 contenidos en las 2009 sucesiones, hallar el menor valor posible de n.
3. Se
tienen 2009 bolitas, algunas blancas y las otras, negras. Todas las bolitas de
un mismo color deberían tener el mismo peso, las blancas más livianas que las
negras. Sin embargo se sabe que hay exactamente una bolita con el color
equivocado, o sea, tiene el peso de una bolita del otro color.
Demostrar que se la puede identificar mediante 7 pesadas en una balanza de dos
platos. (la balanza indica si los dos platos pesan lo mismo o cuál de los dos
pesa más)
4. Hallar todos los enteros n > 1 que se pueden representar como suma de 4 divisores de n-1 positivos y distintos entre sí.
5. Sea ABCD un cuadrilátero convexo, sea I el incentro del triángulo ABD y sea I el incentro del triángulo BDC. Se sabe que los cuadriláteros ABIDy CBID son cíclicos.
Demostrar que las rectas AC, BD e II son concurrentes si y sólo si ABCD es un paralelogramo.
6. Se
tienen 4 varillas verticales. En la varilla 1 hay 2009 CD’s de color a,
en la varilla 2 hay 2009 CD’s de color b y en la varilla 3 hay 2009 CD’s
de color c, formando tres torres. La varilla 4 está vacía.
La movida permitida es pasar el disco superior de una torre a otra varilla de
modo que quede encima de los discos de esa torre, o pasarlo a una varilla vacía.
El objetivo es que queden 2009 discos en la varilla 1 con colores alternados
b, c, a, b, c, a, … (de abajo hacia
arriba), 2009 discos en la varilla 2 con colores alternados c, a,
b, c, a, b, … (de abajo hacia arriba) y 2009 discos
en la varilla 3 con colores alternados a, b, c, a,
b, c, … (de abajo hacia arriba).
Mostrar cómo se puede lograr el objetivo en el menor número posible de movidas.
| Nivel 3 |
1. Hallar todas las parejas (a, b) de números reales con la siguiente propiedad:
Dados los números reales c y d, si las ecuaciones
![]() y
y ![]()
tienen raíces reales, entonces la ecuación
![]()
tiene raíces reales.
2. Sean
A, B, C, D, E, F, G, H,
I nueve puntos en el espacio tales que
A, B, C,
D, E, en ese orden, son los vértices de un pentágono regular de
lado 1.
A, B, F,
G, H, en ese orden, son los vértices de un pentágono regular de
lado 1.
G, F, C,
D, I, en ese orden, son los vértices de un pentágono regular de
lado 1.
Determinar la medida de los lados del triángulo EHI.
3. Una
permutación de los números enteros![]() se
llama d-ordenada si no contiene una subsucesión decreciente de longitud
d.
se
llama d-ordenada si no contiene una subsucesión decreciente de longitud
d.
Demostrar que para todo d tal que
![]() el
número de permutaciones d-ordenadas de
el
número de permutaciones d-ordenadas de
![]() es
a lo sumo
es
a lo sumo ![]()
4.
Hallar todas las funciones ![]() tales
que para todo par (x, y) se verifica
tales
que para todo par (x, y) se verifica
![]()
5. Hallar todos los pares de enteros (a, b) con a, b, tales que a divide a b+1 y b divide a a3-1.
6. Dado
un conjunto de rectángulos, la movida permitida es elegir dos de ellos que
tengan un lado de la misma longitud y unirlos a lo largo de ese lado en un solo
rectángulo. Dos jugadores A y B mueven por turnos, comenzando con un conjunto
inicial de 1000 rectángulos de 1 x 2; A hace la primera movida. Pierde el
jugador que en su turno no puede hacer una movida permitida.
Describir una estrategia ganadora para el jugador B.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |