IX Olimpíada
Matemática Ñandú
Certamen Regional
28 de septiembre de 2000
| primer nivel |
1
Un grupo de personas quieren ir todas juntas de
excursión.
Hay dos agencias que hacen esa excursión: A y B. Las dos
agencias tienen el mismo número de automóviles.
La agencia A tiene 5 autos de 6 asientos y el
resto de 4 asientos.
La agencia B tiene 5 autos de 4 asientos y el resto de 6
asientos.
No pueden ir por la agencia A porque, aunque llenen todos los lugares disponibles, falta lugar para 14 personas.
Yendo por la agencia B llenan todos los lugares disponibles y pueden viajar todos. ¿Cuántas personas forman el grupo?
2
Martín dibujó un rectángulo ABCD con el lado
AB mayor que el lado BC.
Sobre el lado AB marcó el punto R y sobre el lado CD el punto S
de modo que el ABCD quedó dividido en el cuadrado ARSD y el
rectángulo RBCS. El segmento RB mide 6 cm.
El perímetro del rectángulo RBCS es igual a los cinco octavos del perímetro del cuadrado ARSD. ¿Cuál es el perímetro del rectángulo ABCD?
3
Con los dígitos: 1 - 1 - 2 - 2 - 3 - 3 - 4 - 4 se escriben números de 8 cifras.
Por ejemplo: Aldo puede escribir el número 13224341.
los dos 4 separados por cuatro cifras, los dos 3 separados por tres cifras, los dos 2 separados por dos cifras y los dos 1 separados por una cifra.
¿Cuál es el mayor de los números que escribe Bruno ?
| segundo nivel |
1
En la escuela, 5°, 6° y 7° se pueden cursar en el turno mañana o en el turno tarde.
El total de alumnos de 5°, 6° y 7° es 734; en el turno tarde hay 10 alumnos más que en el turno mañana.
El total de alumnos de 5° es 247; en el 5° turno tarde hay 7 alumnos más que en el 5° turno mañana. En 6° hay, en total, 1 alumno más que en 7° .
En 6° del turno mañana hay 5 alumnos más que en 5° del turno mañana. ¿Cuántos alumnos hay en 7° del turno tarde?
2
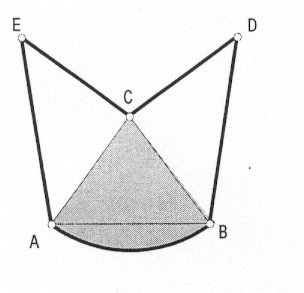
El triángulo ABC es isósceles con AC = BC y <ACB = 4/3 <CBA
(<ACB indica el ángulo ACB)
AB es un arco de circunferencia de centro C y radio CA. La parte sombreada de la figura tiene aproximadamente 22,61cm2 de área.
Los triángulos ECA y BCD son isósceles, rectángulos e iguales entre sí.

3
Los padres de Javier quieren comprar un departamento que cuesta $ 120000 pero no disponen de todo el dinero.
Pagarán una parte al contado y el resto en dos partes iguales: la primera mitad, con el 20% de recargo, en 30 cuotas iguales y la otra mitad, con el 5% de recargo, en 15 cuotas iguales. Por cada una de las 15 últimas cuotas deberán pagar $ 2184.
¿Qué porcentaje del valor del departamento
pagaron al contado?
¿Cuánto deberán pagar por cada una de las primeras 30 cuotas?
| tercer nivel |
1
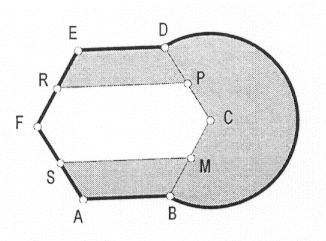
ABCDEF es un hexágono regular.
M, P, R y S son los puntos medios de los lados BC, CD, EF y FA, respectivamente.
BD es un arco de circunferencia de centro C y radio CD.
El perímetro de toda la figura es de aproximadamente 65,5 cm.
¿Cuál es el área de la parte sombreada?
2
Juan sumó 99 números impares consecutivos y obtuvo como resultado 12375.
¿Cuál es el mayor de los números que sumó Juan?
Por ejemplo:
5 y 7 son dos impares consecutivos;
37; 39; 41 y 43 son cuatro impares consecutivos.
3
Un comerciante compró tres artículos por un total de $ 440 y después los vendió y obtuvo una ganancia del 30%.
Uno de los artículos le dio una ganancia del 20%, otro una ganancia del 25% y el tercero una ganancia del 50%.
Lo que pagó por el artículo que le dio menor porcentaje de ganancia es igual a la suma de los precios de venta de los otros dos artículos.
¿Cuánto pagó el comerciante por cada uno de los tres artículos?
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |