 1
1IX Olimpíada
Matemática Ñandú
Certamen Nacional
2 de noviembre de 2000
| primer nivel |
 1
1
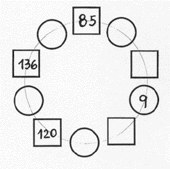
Andrés escribió un número entero en cada circulo y después puso en cada cuadrado el resultado de multiplicar los números que estaban en los dos círculos vecinos.
Algunos de los números se borraron.
Completa los cuadrados y círculos vacíos con los números que había escrito Andrés. Explica cómo los encontraste.
2
Tomás tiene tres cajas: una roja, una verde y una azul, con bolitas.
Pasa un tercio de las bolitas de la caja roja a la caja verde. Después, pasa un cuarto de las bolitas que hay ahora en la caja verde a la caja azul. Por último pasa un décimo de las bolitas que hay ahora en la caja azul a la caja roja.
Cuando termina de hacer estos cambios tiene 18 bolitas en cada caja. ¿Cuántas bolitas tenía inicialmente en cada caja?
 3
3
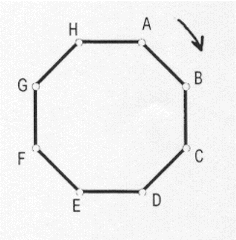
Una hormiga camina por el borde de un plato de 8 lados iguales como el de la figura.
Cada lado del plato mide 14 cm. La hormiga sale del vértice A y camina en el sentido que indica la flecha, siempre por el borde del plato. Hace la primer parada a 6 cm del vértice A y después, cada 6 cm hace una parado. En total hace 2000 paradas. ¿Cuántas veces para en el vértice A?
¿En qué otros vértices hace la misma cantidad de paradas que en A?
| segundo nivel |
1
Un tren parte de Azul con 134 pasajeros entre hombres, mujeres y niños. Para en varias estaciones; cada vez que para, bajan 2 hombres y 1 mujer y suben 4 niños.
Al llegar al final del recorrido hay, en total, 143 pasajeros:
el número de niños es una vez y media el número de hombres,
el número de mujeres es la mitad del número de niros.
¿ Cuántos hombres, mujeres y ninos habla en el tren cuando partió de Azul?
 2
2
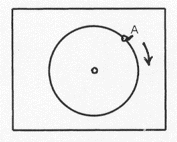
En la pantalla de la computadora se ve una marca A y un disco que puede girar sobre su centro, como en la figura. El disco es blanco y el punto del borde que coincide con la marca A es de color rojo.
Ceda vez que se aprieto la tecla E, el disco gira 15' en el sentido de las agujas del reloj y, cuando se detiene, cambia el color del punto del borde del disco que coincide con la marca A, de la siguiente manera: si es blanco, cambia a rojo; si es rojo, cambio a azul; si es azul, cambia a rojo. Después de apretar la tecla E 2000 veces, ¿cuántos puntos rojos y cuántos puntos azules hay en el borde del disco?
¿Cuál es el menor número de veces que hay que apretar la tecla E para que haya más puntos ázules que rojos?
 3
3
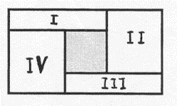
Inés dibuja todos los rectángulos de 264 cm2 de área y lados de longitudes enteras (en cm) que puede partir en un cuadrado y cuatro rectángulos, todos de lados de longitudes enteras, como en la figura.
El cuadrado está ubicado en el centro, el rectángulo I es igual al rectángulo III y el rectángulo II es igual al rectángulo IV.
¿Cuáles son los rectángulos que dibujó Inés?
En cada uno de esos rectángulos, ¿cuál es el área de cada uno de los cuadrados ubicados en el centro?
| tercer nivel |
1
La distancia entre Ciudad Vieja y Ciudad Nueva es de 480 krn. Los trenes A y B van de Ciudad Viejo a Ciudad Nueva.
El tren B tarda una hora y media más que el A en recorrer la distancia entre las dos ciudades.
La velocidad del tren B es 16 km/h menor que la velocidad del tren A.
¿Cuál es la velocidad de cada tren?
 2
2
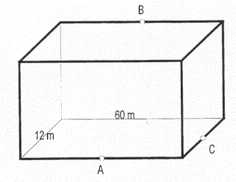
Un galpón tiene forma de prisma recto de base rectangular como el de la figura.
A, B y C son los puntos medios de las aristas que los contienen.
El galpón tiene 60 m de frente, 12 m de fondo y 5 m de altura.
En el interior se coloca un alambre que va de A a B y de B a C.
¿Cuál es la longitud del alambre?
3
En un torneo de ajedrez se inscriben 12 jugadores.
Los participantes son tres pares de hermanos varones y tres pares de hermanas mujeres.
Los hermanos Álvarez están casados con las hermanas Bianco.
Los hermanos Fernández están casados con las hermanas Caril. Los hermanos Pérez están casados con las hermanas Pusso.
Cada partido de la primera ronda se disputará entre un hombre y una mujer pero, ninguna mujer puede enfrentarse ni con su esposo ni con el esposo de su hermana.
¿De cuántas maneras se pueden armar los 6 partidos de la primera ronda?
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |