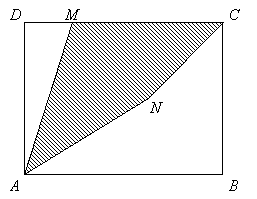
M es un punto de CD tal que MC = BC
N es el punto medio de MB
¿Qué fracción del rectángulo ABCD representa el cuadrilátero AMCN?
VI
Olimpíada Matemática Ñandú. 1997Certamen Nacional
Primer
nivel1
Gabi tiene 32 fichas:
| 4 fichas tienen escrito el número "1", | 4 fichas tienen escrito el "2", |
| 4 fichas tienen escrito el "3", | 4 fichas tienen escrito el "4", |
| 4 fichas tienen escrito el "5", | 4 fichas tienen escrito el "6", |
| 4 fichas tienen escrito el "7" y | 4 fichas tienen escrito el "8". |
Gabi quiere armar 16 grupos de 2 fichas cada uno, de
modo que no haya grupos repetidos y que cuando sume los
números de las fichas de cada grupo, el resultado sea
siempre un número par.
¿Puede hacerlo? Explica por qué.
2
Tomás saca todas las hojas múltiplos de 7 de su
cuaderno.
Luego saca, de lo que quedó, todas las hojas múltiplos
de 5.
Finalmente, de lo que quedó, saca todas las hojas
múltiplos de 3.
Después de todo esto, a Tomás le quedan 25 hojas en su
cuaderno.
¿Cuántas hojas tenía inicialmente el cuaderno de
Tomás?
3
| ABCD rectángulo, 5 AB = 6 BC M es un punto de CD tal que MC = BC N es el punto medio de MB ¿Qué fracción del rectángulo ABCD representa el cuadrilátero AMCN? |
 |
Segundo
nivel1
Daniel quiere comprar 2 libros de entre los 7 que le
gustan.
Cada libro cuesta una cantidad entera de $ ;
El precio más barato es $ 2.
Daniel observa que las distintas elecciones de dos
libros, entre los 7 que le gustan, cuestan cantidades
distintas de dinero.
¿Cuánto debe costar cada libro para que la suma de los
precios de los 7 libros sea la menor posible?
2
Dibuja un cuadrado ABCD.
Marca un punto P en el lado BC y un
punto Q en el lado CD, de modo que los
triángulos APB y AQD tengan áreas
distintas y, además, el área del cuadrilátero APCQ
sea el triple de la suma de las áreas del triángulo APB
y del triángulo AQD.
Explica cómo elegiste los puntos y por qué las áreas
de las tres figuras cumplen las condiciones pedidas.
3
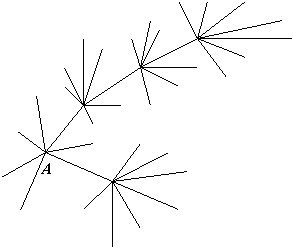
| A es el punto de la
figura. Se dibujan 7 segmentos con un extremo en A. Se eligen algunos extremos libres de los segmentos dibujados (distintos de A; A no es un extremo libre) y se dibujan 7 segmentos con un extremo en cada uno de los puntos elegidos. (ver ejemplo en la figura) Se continúa este proceso. ¿Es posible, después de varios pasos, tener:
Explica por qué. |
 |
Tercer
nivel1
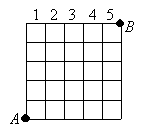 Juan
tiene que llevar una ficha desde A hasta B
moviéndola por las líneas de la cuadrícula del tablero
de la figura. Puede moverse hacia arriba, hacia abajo,
hacia la izquierda o hacia la derecha.
Juan
tiene que llevar una ficha desde A hasta B
moviéndola por las líneas de la cuadrícula del tablero
de la figura. Puede moverse hacia arriba, hacia abajo,
hacia la izquierda o hacia la derecha.
Cada vez que la ficha se mueve en sentido horizontal,
Juan anota el número de la columna que atraviesa.
Cuando la ficha llega a B, Juan multiplica todos
los números que anotó.
¿Hay algún camino para el cual el resultado es 4320?
¿Hay algún camino para el cual el resultado es 6000?
Si la respuesta es no, explicar por qué.
Si la respuesta es si, mostrar el camino.
2
Ariel, Bruno y Carla tienen, entre los tres, 35
monedas.
los tres tienen monedas de $ 1, de 50 centavos y de 25
centavos;
en total tienen $ 17.
Los tres tienen igual cantidad de monedas de $ 1.
Ariel tiene el doble de monedas de 50 centavos que Bruno
y Carla juntos.
Bruno tiene 2 monedas de 25 centavos más que Ariel.
Carla tiene 4 monedas de 25 centavos más que Bruno.
¿Cuántas monedas de cada clase tiene cada uno?
Dar todas las soluciones posibles.
3
| La circunferencia de centro O tiene
5 cm de radio. El triángulo ABC tiene 84 cm de perímetro y sus lados son tangentes a la circunferencia de centro O. Los arcos de circunferencia con centro en cada vértice del triángulo tienen 4 cm de radio. ¿Cuál es el área de la zona rayada? |
 |
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |