Certamen Nacional

1. En el juego de "PAN Y QUESO" dos chicos dicen PAN, QUESO, en forma alternada y van uno al encuentro del otro por la línea pintada, poniendo cada vez un pie pegadito al otro.

Al decir PAN, el primer jugador adelanta un pie; al decir QUESO, lo hace el segundo. Gana el que pisa primero al otro.
En el recreo armaron dos equipos de tres chicos para jugar.
En el equipo de Aníbal, los tres calzan 40(40cm); en el equipo de Blas, uno calza 33(33cm), otro calza 34(34cm) y el tercero calza 35(35cm).
La línea pintada mide 775 cm. Cada equipo elige un chico para jugar.
Si inicia el juego el equipo de Aníbal, ¿a quién elige Blas para ganar?
Si inicia el juego el equipo de Blas, ¿a quién elige Blas para ganar?

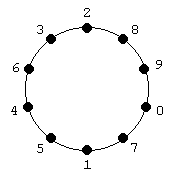
2. En un aro circular hay chapitas numeradas como muestra la figura. Cuando se elige un grupo de chapitas consecutivas, se escribe el número que queda formado leyendo las cifras de las chapitas en el sentido de las agujas del reloj. Por ejemplo: si se elige el grupo formado por el 2, el 8 y el 9, se escribe el número 289. Separar todas las chapitas en tres grupos de modo que al escribir los números que quedan, el producto de los dos primeros sea el tercero.

3. Un rompecabezas tiene 81 piezas cuadradas de 1cm de lado cada una. Usando todas las piezas se arman dos rectángulos distintos de mode que el perímetro del más grande sea el doble del perímetro del más chico.
¿Cuáles son el largo y el ancho de cada uno de los dos rectángulos.

1. Un comerciante compra bolsas de papas que siempre pesan un número entero de kilos.
Recibió cuatro bolsas todas de distinto peso y como tiene una balanza que sólo marca pesos mayores de 100 kg las pesa de a dos.
Sólo consigue cuatro resultados: 101, 112, 116 y 127 porque los otros dos pesos son menores de 100 kg.
Con esta información se puede conocer el peso de cada una de las cuatro bolsas.
¿Cuáles son esos pesos?

2. El arco AB es un cuarto de una circunferencia de centro O y radio 10cm. Los arcos OA y OB son semicircunferencias. ¿Cuál es el área de la región sombreada?

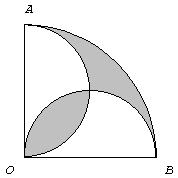3. Juan y Pedro ponen "1" y "2" en los vértices de un hexágono regular como el de la figura. Cada uno en su turno pone un uno o un dos, a su elección. Después de seis jugadas, cuando el juego termina, un árbitro pone, en cada lado del hexágono, el producto de los números de los dos vértices. Para finalizar, suma los doce números escritos. Si la suma es impar, gana Juan; si es par, gana Pedro. Uno de los dos puede ganar siempre, no importa lo bien que juegue el otro. Si empieza Juan, ¿quién gana y cuál es su estrategia ganadora?

1. En un recipiente cúbico de 1m de arista hay 3cm de agua. Se introduce un cubo de polomo en el recipiente y, cuando queda apoyado en el fondo, la altura del agua en el recipiente es de 4cm.
¿Cuál es la longitud de la arista del cubo de plomo?

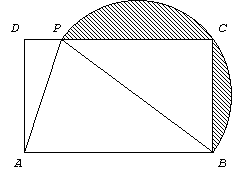
2. ABCD es rectángulo. P es un punto de CD y PB = AB. El arco PCB es una semicircunferencia. Area del triángulo BCP = 4 Area del triángulo APD. Area del triángulo ABP = 4,8 dm2. ¿Cuál es el perímetro de la zona rayada?

3. Ariel, Germán, Martín y Raúl son integrantes del centro de estudiantes y uno de ellos es, además el presidente del centro y compañero de curso de uno de los otros tres.
En la fiesta de fin de curso, cada uno de ellos vendió bonos contribución.
Ariel sólo vendió bonos de $3 , Germán bonos de $4 , Martín de $6 y Raúl de $8. Cada uno vendió un número distinto de bonos.
El presidente del centro vendió el mayor número de bonos y recaudó en total $72. Su compañero de curso vendió el menor número de bonos y recaudó $24 en total. Entre todos recaudaron $161.
¿Quién es el presidente y quién su compañero de curso?

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar