20º Olimpíada
Matemática Ñandú
Certamen Nacional - 2011
Primer nivel
1.
Andrés
compra 240 fichas, algunas rojas, algunas azules y otras verdes.
Las rojas cuestan $ 4 cada una, las azules, $ 2 cada una y las verdes, $ 1 cada
una. Gasta $ 640 en fichas.
Si las azules costaran como las rojas y las rojas costaran como las azules,
Andrés gastaría $ 560.
¿Cuántas fichas de cada clase compra Andrés ?

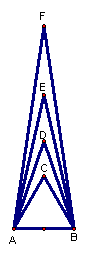
2. En la figura: ABC es un triángulo equilátero;
ABD, ABE y ABF son triángulos isósceles.
AD = DB =
![]() AB;
AE = EB =
AB;
AE = EB =
![]() AD
AD
AF
= FB = ![]() AE;
Perímetro de ABF = 124 cm.
AE;
Perímetro de ABF = 124 cm.
¿Cuáles son los perímetros de ABC; ABD y ABE?
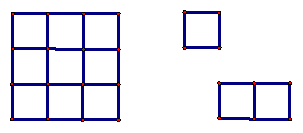 3.
Hay 9 piezas
cuadradas de 1x1 blancas;
3.
Hay 9 piezas
cuadradas de 1x1 blancas;
1 pieza rectangular de 1x2 roja y
1 pieza rectangular de 1x2 azul.
Se quiere cubrir este cuadrado de 3x3
usando algunas de esas piezas.
¿De cuántas maneras puede hacerse?
Da todas las posibilidades.
Segundo nivel
1.
Una florista ofrece tres tamaños de arreglos florales que contienen rosas de
color blanco, rojo y amarillo.
Cada arreglo pequeño contiene 1 rosa blanca, 3 rojas y 3 amarillas.
Cada arreglo mediano contiene 2 rosas blancas, 4 rojas y 6 amarillas.
Cada arreglo grande contiene 4 rosas blancas, 8 rojas y 6 amarillas.
Un día la florista empleó 72 rosas blancas, 150 rojas y 144 amarillas para
preparar los pedidos de estos tres tipos de arreglos. ¿Cuántos arreglos de cada
tamaño preparó?
Si vendió cada arreglo pequeño a $ 10, cada mediano a $ 20 y cada grande a $ 30,
¿cuánto dinero recaudó por esos pedidos?
2.
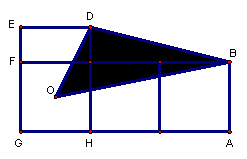
La figura ABCDEG está formada por tres cuadrados iguales y el rectángulo CDEF.
DE=2CD; O es el centro del cuadrado CFGH.
El perímetro de ABCDEG es 108 cm.
¿Cuál es el área de la región sombreada?
3. Los números
impares 1, 3, 5,7,… se colocan en 5 columnas siguiendo el esquema mostrado aquí
abajo. ¿En qué fila y en qué columna aparecen
a) el
509? b) el 2011?
Explica por qué.
|
|
1 |
3 |
5 |
7 |
|
15 |
13 |
11 |
9 |
|
|
|
17 |
19 |
21 |
23 |
|
31 |
29 |
27 |
25 |
|
|
|
33 |
35 |
37 |
39 |
|
47 |
45 |
43 |
41 |
|
|
|
49 |
51 |
53 |
55 |
|
… |
… |
… |
… |
… |
Tercer nivel
1.
Se prepara dulce que se
envasa en frascos grandes de 900 g, en frascos pequeños de 450 g y en frascos
individuales de 30 g. Al envasarlo se pierde el 10 %.
La cantidad de frascos pequeños es más de una vez y media y menos del doble de
la cantidad de frascos grandes.
En frascos pequeños se envasa igual cantidad de kilos que en frascos
individuales.
Los
frascos grandes se venden a $ 25 cada uno, los pequeños a $ 15 cada uno y los
individuales a $ 1,50 cada uno. Se recaudan $ 625.
¿Cuántos frascos de cada tamaño se envasan? ¿Cuántos kg de dulce se habían
preparado?
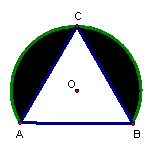
2.
En la figura, ABC es un
triángulo equilátero inscripto en la circunferencia de centro O y radio OA.
El perímetro del triángulo ABC es 62,34 cm.
¿Cuál es el área y cuál es el perímetro de la región sombreada ?
3. Hay 5 lámparas en línea, controladas por 5 teclas (A; B; C; D y E)
|
Q |
Q |
Q |
Q |
Q |
|
A |
B |
C |
D |
E |
Cada lámpara puede estar:
apagada, con luz suave o con luz fuerte.
Cada tecla cambia de estado la lámpara que está arriba suyo, la de la izquierda
y la de la derecha.
Al accionar la tecla, cada una de las lámparas afectadas cambia: de apagada a
luz suave, de luz suave a luz fuerte o de luz fuerte a apagada.
Al principio las 5 lámparas están apagadas. Accionando la menor cantidad de
teclas se quiere llegar a este orden: luz fuerte; luz suave; luz fuerte; luz
suave; luz fuerte.
¿Qué teclas se pueden accionar? Da todas las posibilidades.
En cada caso muestra, paso a paso, los cambios de estado.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |