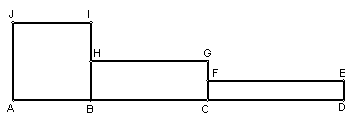
19º Olimpíada
Matemática Ñandú
Certamen Regional
2 de septiembre
Primer nivel
1. Marcelo tiene $ 450 en billetes de $2; de $5 y de $10.
Tiene 62 billetes entre los de $2 y los de $5.
Tiene 48 billetes entre los de $5 y los de $10.
¿Cuántos billetes de cada clase tiene?
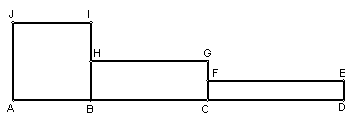
2. En la figura, de 378 cm de perímetro, ABIJ es un cuadrado.
H es punto medio de BI, F es punto medio de CG.
Los rectángulos BCGH y CDEF tienen igual perímetro que el cuadrado ABIJ.
¿Cuál es el perímetro del cuadrado ABIJ?
3. La abuela de Sofi preparó mermeladas de 6 gustos distintos que guarda en
un frasco de 1 kilo, dos frascos de medio kilo y tres frascos de un cuarto kilo.
En los frascos de un cuarto kilo guardó las mermeladas de frutilla, manzana y pomelo.
En los frascos de medio kilo guardó la de ciruela y la de naranja.
En el frasco de 1 kilo guardó la mermelada de durazno.
Quiere acomodar los 6 frascos en un estante, de modo que los de igual capacidad estén juntos.
¿De cuántas maneras distintas puede hacerlo?
Segundo nivel
1.
De un grupo de personas, ![]() son
mujeres.
son
mujeres.
Si hubiese el doble de mujeres y el mismo número de varones, habría 45 mujeres más que varones.
¿Cuántos varones hay en el grupo?

2.
En la figura:
BCDE es un cuadrado de 450 cm2 de área,
AOEG es un rectángulo y BEFG es un paralelogramo.
Las diagonales del cuadrado se cortan en O.
El área del triángulo EFG es 292,50 cm2.
¿Cuál es el área de ABEFG?
¿Cuál es el perímetro del cuadrilátero ABEG?
3. Queremos escribir 165 como suma de varios números enteros consecutivos.
Por ejemplo: 82 y 83 son números enteros consecutivos y 165 = 82 + 83.
¿Hay otras maneras? Da todas las posibilidades.
Tercer nivel
1. Dos jarras idénticas se llenan con café y leche.
En la primera jarra hay 3/5 partes de leche, el resto es café.
En la segunda jarra hay 3/4 partes de leche, el resto es café.
De la primera jarra se consume la tercera parte y se completa con la mezcla de la segunda jarra.
¿Cuál es ahora el porcentaje de café en la primera jarra?
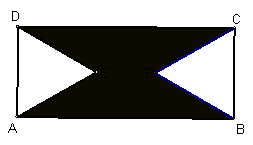
2. En la figura, ABCD es un rectángulo; AED y BCF son triángulos equiláteros . 12 BC = 5 AB.
El área de la parte sombreada es 613,60 cm2.
¿Cuál es el perímetro del cuadrilátero ABFE? ¿Cuál es el área del cuadrilátero ABCE?
3. Para su cumpleaños, Sofía decide comprar sándwiches para comer con sus amigos y amigas.
Si compra 60 sándwiches no le alcanza para que cada chica coma 5 sándwiches y cada chico coma 6 sándwiches.
Si compra 80 sándwiches, cada chica puede comer 6 sándwiches, cada chico puede comer 7 sándwiches y le sobra.
¿Cuántos amigos y cuántas amigas tiene Sofía? Da todas las posibilidades.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |