19º Olimpíada Matemática Ñandú
Certamen Nacional - 2010

Primer nivel

1. Una empresa transportó 6240 toneladas de alimentos utilizando, siempre a su máxima capacidad, 5 camiones grandes y 10 camiones pequeños.
Los camiones grandes tienen 4 toneladas de capacidad y los pequeños, 1 tonelada y media.   
Cada camión hizo siempre el mismo número de viajes por día.
Los camiones pequeños hicieron un viaje más por día que los camiones grandes.
En cierta cantidad de días la empresa transportó 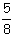 del total.  El resto lo transportó en 6 días menos.

¿Cuántos días  en total tardó la empresa para transportar todos los alimentos?
¿Cuántos viajes por día hizo cada camión grande y cuántos cada camión pequeño?

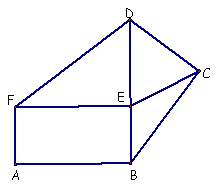
2. ABEF es un rectángulo, AB = 2 BE.
CDE es un triángulo isósceles;  CD=DE.
Los triángulos BCD y FED son iguales, BC = FE.
Los triángulos BCE y CDE tienen igual perímetro.
El perímetro de ABDF es 288 cm.
¿Cuál es el perímetro de ABCDF?
¿Cuál es el perímetro de BCD?

3.a) Juan escribe los números del 1 al 12, uno en cada casilla del tablero de manera que la suma de los 4 números de cada fila es la misma para las 3 filas. Muestra una manera de hacerlo.
¿De cuántas maneras se puede completar la primera fila  empezando con el 12  y con los otros tres números ordenados de mayor a menor?
Para cada una, muestra un tablero posible.

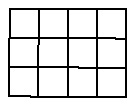
b) ¿Podrá Juan poner los 12 números en el tablero de manera que la suma de los 3 números de cada columna sea la misma  para  las 4 columnas?
Si es posible, muestra cómo. Si no es posible, explica por qué.

Segundo  nivel

1. Bea compró una computadora y un teléfono celular.  Con los $ 2880 que tenía, pagó la tercera parte del valor de cada objeto.
Al mes siguiente pagó las dos quintas partes de lo que le faltaba pagar por la computadora y todo lo que le faltaba pagar por el teléfono celular.
La deuda que le quedó la pagará, con un recargo de la quinta parte de la misma, en 8 cuotas mensuales de $ 351 cada una.
¿Cuál era el precio de la computadora y cuál el del teléfono celular?
¿Cuánto habrá pagado Bea en total por la computadora cuando pague la última cuota?

2. En la figura:

         AC = 4 AB
     CE = 6 CD
     BE = 3 EG
     ABEF es un paralelogramo de 108 cm² de área.
     ¿Cuál es el área del triángulo BDG?

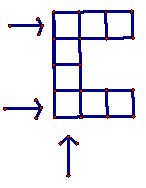
3. Juan escribe los números del 1 al 8, uno en cada casillero, sin repetir ninguno, de modo que si suma los tres números de cada una de las filas
indicadas por las flechas y suma los cuatro números de la columna indicada por la flecha, las tres sumas dan el mismo resultado.
¿Cuáles son los valores que pueden tener estas tres sumas? Para cada suma, muestra cómo puede colocar Juan los números en los casilleros.
Da todas las posibilidades.

Tercer nivel

1. Ana compra comestibles y artículos de limpieza en el supermercado, dos veces por mes.
Este mes, la primera vez, por una promoción, le hicieron el 20 % de  descuento sobre los artículos de limpieza; además, por pagar con tarjeta de
débito tuvo un 15 % de descuento sobre el total; pagó $ 357.
La segunda vez, le hicieron el 20 % de descuento en comestibles y además, por pagar con tarjeta de crédito tuvo un 10 % de descuento sobre el
total; pagó $ 468.
Leyendo los tickets del supermercado, Ana descubrió que si no le hubieran hecho ningún descuento ninguna de las dos veces, la primera vez habría pagado $ 490 y ese mes habría gastado un total de $ 670 por la compra de comestibles en el supermercado.
Sin descuentos, ¿cuánto habría gastado en comestibles y cuánto en artículos de limpieza cada vez?

2. Se dibuja un triángulo ABC tal que 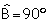  , 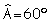  y  BC = 6 cm.
Con centro A y radio AC se traza un arco de circunferencia que corta a la  semirrecta 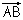en el punto D.
Con centro B y radio BC se traza un arco de circunferencia que corta a la semirrecta  en el punto E.   
Se sombrean:
la región I limitada por los segmentos BC y BD, y el arco CD y
la región II  limitada por los segmentos AC y AE, y el arco CE.
¿Cuál es el área de cada una de las regiones sombreadas?

3  Un triángulo equilátero de lado 3 se dividió en 9 triangulitos, también equiláteros, de lado 1.
Se quieren colocar los números del 1 al 9, uno en cada triangulito, de manera que en todo triángulo equilátero de lado 2 la suma de los números sea la misma.
¿Qué sumas se pueden obtener?  ¿Cuál es la  menor?  ¿Cuál es la mayor?
Para cada suma, muestra cómo se pueden colocar los números.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar