19º Olimpíada
Matemática Ñandú
Certamen Interescolar
13 de mayo 2010
Primer nivel
. Un ascensor sale de la planta baja con 7 personas. Para en todos los pisos.
En cada piso suben 2 personas.
En los pisos pares bajan 3 personas y en los pisos impares no baja ninguna.
¿Cuántas personas hay en el ascensor antes de que se abra la puerta en el piso 11?

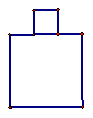
2. Con dos piezas cuadradas se armó esta figura.
El lado del cuadrado pequeño mide 5 cm.
El lado del cuadrado grande es el triple del lado del
cuadrado pequeño.
¿Cuál es el perímetro de la figura?
3. Durante las vacaciones siempre uso calzas, pollera, remera y anteojos de sol.
Tengo que ponerme la remera antes que los anteojos, y las calzas antes que la pollera.
¿Durante cuántos días me puedo vestir en un orden diferente?
Explica en qué orden se viste cada día.
Segundo nivel
Raúl tiene que tomar un remedio que viene en cajas de dos clases:
de 16 comprimidos, que cuestan $ 33 cada una y de 20 comprimidos, que cuestan $ 40 cada una.
Debe tomar 2 comprimidos por día durante 6 semanas. Quiere comprar todas cajas de la misma clase. ¿Cuáles y cuántas cajas debe comprar para gastar lo menos posible?
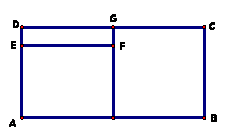
2. El rectángulo ABCD está formado por
dos cuadrados iguales como muestra la figura.
AB = 40 cm. El perímetro del rectángulo DEFG es ![]() del perímetro de ABCD.
del perímetro de ABCD.
¿Cuánto miden los lados del rectángulo DEFG?
3. Susana pensó tres números, los sumó y obtuvo 100.
Uno de los números es múltiplo de 11 y los otros dos son múltiplos de 8.
¿Cuáles pueden ser los tres números que pensó Susana?
Da todas las respuestas posibles.
Tercer nivel
1. En básquet se pueden anotar 3 puntos (triple), 2 puntos (doble) o 1 punto (tiro libre) cada vez que se encesta en el aro.
En un partido, un equipo obtuvo 86 puntos y habían encestado 40 veces.
Si se sabe que obtuvo 12 triples, ¿cuántos dobles y cuántos tiros libres encestaron?
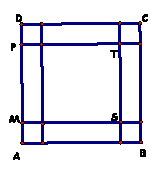
2. El cuadrado ABCD tiene 168 cm de perímetro.
En cada vértice se recortó un cuadradito de 7 cm de lado.
¿Cuál es el área del rectángulo STPM?
3. Se quieren distribuir 25 caramelos iguales en tres frascos: uno rojo, uno azul y uno verde,
de modo que el frasco azul tenga por lo menos 2 caramelos más que el rojo y
el frasco verde tenga más del doble de los caramelos que tiene el azul.
¿De cuántas maneras se puede hacer? Indica cuáles son.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |