XVIII Olimpíada Matemática
Ñandú
Certamen Regional
17 de septiembre de 2009
Primer Nivel
1 Pérez y
Capria son socios en una empresa. Capria quiere repartir entre los empleados su
parte en las ganancias de este fin de semana.
Si les diera $ 125 a cada uno, le sobrarían $ 75. En cambio, si les diera $ 150
a cada uno, le faltarían $ 450. ¿Cuántos empleados tiene la empresa?
Si a Capria le corresponde la tercera parte de las ganancias, ¿a cuánto
ascienden las ganancias de este fin de semana?
2
Se tienen 3 piezas de cartón: un rectángulo, un triángulo isósceles y un
cuadrado.
El triángulo tiene un lado igual al lado del cuadrado.
El rectángulo tiene dos lados iguales al lado del cuadrado.
El perímetro del triángulo es 7 cm menor que el perímetro del cuadrado.
La suma de los perímetros de las 3 piezas 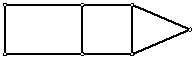 es
189 cm.
es
189 cm.
La figura, que se armó con estas piezas, tiene 129 cm de perímetro.
¿Cuánto miden los lados de cada una de las piezas?
3 Se quiere cambiar
un billete de 10 pesos en monedas de 1 peso ; 50 centavos y 25 centavos.
¿De cuántas maneras se puede hacer si se quiere tener, por lo menos, una moneda
de cada clase? Indica todas las posibilidades.
Segundo Nivel
1
Daniel tenía unos pesos ahorrados.
El lunes sacó $ 20 y después agregó una cantidad igual a la mitad de lo que
le quedaba.
El martes también sacó $ 20 y después agregó una cantidad igual a la mitad de lo
que le quedaba.
El miércoles contó cuánto dinero tenía ahorrado y resultó ser el doble de lo que
tenía al principio.
¿Cuánto dinero tenía inicialmente?
2
En la figura: ABGF es un
cuadrado,
DEFG es un rectángulo,
BCG y CDG son triángulos rectángulos.
 CG
mide 12 cm.
CG
mide 12 cm.
El perímetro de ABCF es 80 cm.
El perímetro del triángulo BCG es 48 cm.
El área del rectángulo DEFG es 144 cm2.
El perímetro del triángulo CDG es 36 cm.
¿Cuál es el perímetro y cuál es el área de la figura ABCDE?
3
Con los dígitos 1 – 2 – 3 – 4, Dany arma una clave numérica de 6 cifras.
Utiliza dos de esos dígitos dos veces y los otros dos dígitos una sola vez.
El número que arma termina en 4 y es múltiplo de 4.
¿Cuántas y cuáles son las claves que puede armar Dany?
Tercer Nivel
1
En la escuela, en séptimo grado hay 7 chicos menos que en sexto.
Este lunes, el 30 % del total de los chicos de quinto, sexto y séptimo,
estuvieron con gripe.
Hubo 33 enfermos en total.
Estuvieron enfermos el 40 % de los chicos de quinto, el 25 % de los chicos de
sexto; en séptimo grado hubo 3 enfermos menos que en sexto.
¿Cuántos chicos hay en cada grado?
2
En una semicircunferencia
de centro O y diámetro AB, se marca el punto C de modo que:

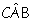 =30º
y
=30º
y 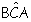 =90º
=90º
Si el arco AC tiene
50,24 cm de longitud,
¿cuál es el área de la región sombreada?
3
Los asientos del avión se
identifican con el número de la fila y la letra de la columna.
En el sector de los 9 asientos de las filas 1 – 2 – 3 y columnas A – B – C, hay
que ubicar 6 mantas: 2 rojas y 4 azules.
Nunca hay más de una manta por asiento.
Las dos rojas se colocan en la misma fila y en asientos consecutivos.
Las azules se ubican de modo tal que no queda ninguna fila ni ninguna columna
del sector vacía.
¿De cuántas maneras distintas pueden ubicarse las mantas? Descríbelas todas.
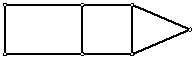 es
189 cm.
es
189 cm.
