XVII Olimpíada Matemática Ñandú
Certamen Regional

4 de septiembre de 2008

Primer Nivel

1 En el tablero de la figura se colocan fichas rojas y fichas azules del siguiente modo:
- en cada una de las casillas de las esquinas se pone igual cantidad de fichas rojas,
- la casilla central se deja vacía,
- en cada una de las otras casillas se pone igual cantidad de fichas azules.
En total, en la primera fila hay 41 fichas. ¿De cuántas maneras distintas se pudo haber completado el tablero? En cada caso, indica: a) cuántas fichas rojas y cuántas azules se colocaron en cada casilla, b) cuántas fichas se colocaron en total.

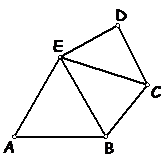
2 En la figura, ABE es un triángulo equilátero,
BC = CD = DE
BE = CE
El perímetro del triángulo BCE es 28 cm .
El perímetro del triángulo CDE es 26 cm .
¿Cuál es el perímetro del polígono ABCDE?

3 El maestro quiere repartir 576 figuritas entre 10 de sus alumnos, 4 varones y 6 mujeres.
Para varones tiene la mitad de figuritas de las que tiene para mujeres.
A medida que van llegando: a cada mujer le da 2 figuritas menos de las que le dio a la anterior, a cada varón le da 6 figuritas más de las que le dio al anterior.
¿Cuántas figuritas le dio a cada alumno?

Segundo Nivel

1 En el quiosco hay paquetes de caramelos de tres gustos: miel, leche y fruta.
Se venden a $ 5 los de miel, $ 6 los de leche y $ 4 los de fruta.
Si se venden todos los paquetes se obtienen $ 462. En total hay 96 paquetes.
Si hubiera el doble de paquetes de leche, el doble de paquetes de fruta y la misma cantidad de paquetes de miel, habría en total 162 paquetes.
¿Cuántos paquetes de caramelos de cada gusto hay en el quiosco?

2 En el rectángulo ABCD, M es el punto medio del lado BC y N es un punto del lado CD.
El área del triángulo ABM es 27 cm 2 .
El área del triángulo AND es 9 cm 2 .
¿Qué parte de CD es DN?
¿Cuál es el área del triángulo AMN?

3 Ana tiene 10 monedas de $ 1 y 6 cajitas de distintos colores: azul, blanca, celeste, negra, roja y verde. Quiere guardar las monedas en las cajitas de manera que ninguna quede vacía. ¿De cuántas maneras puede hacerlo? Indica cuáles son.

Tercer Nivel

1 Un automovilista va de A hasta B, distantes 240 km , a velocidad constante.
Al regreso hace la cuarta parte del camino a la misma velocidad que llevaba a la ida y en el resto del camino, reduce su velocidad a la mitad.
Si en el viaje de regreso tarda 4 horas y 40 minutos, ¿a cuántos kilómetros por hora iba a la ida?

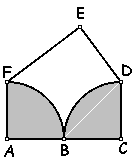
2 Los arcos FB y BD son cuartos de circunferencias de igual radio.
DE es perpendicular a EF
DE = 12 cm
El perímetro de la región sombreada es 71,4 cm .
¿ Cuál es el área y cuál es el perímetro de la región no sombreada?

3 Usando 3 colores: azul, rojo y verde, se quieren pintar todos los triángulos de la figura de modo que dos triángulos que tienen un segmento común, no sean del mismo color.
¿De cuántas formas puede hacerse?
Indica cuáles son.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar