16º Olimpíada
Matemática Ñandú
Certamen Nacional - 2007
Primer nivel
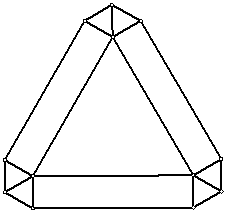1. En
la figura todos los triángulos son equiláteros. El
perímetro de cada rectángulo es el cuádruple
del perímetro de un triángulo pequeño.
El triángulo grande tiene 90 cm de perímetro.
a)
¿Cuál
es el perímetro de la figura?
b)
¿Es
posible dibujar una figura como esta que tenga 2007 cm de perímetro, de modo que:
todos
los triángulos sean equiláteros, el perímetro
de cada rectángulo sea el cuádruple del
perímetro de un triángulo pequeño y todos
los lados tengan longitudes enteras?
Si es posible, indicar la longitud del lado del triángulo grande. Si
no es posible, explicar por qué.
2.
En la escuela los alumnos de quinto, sexto y séptimo son, en total, 349.
En séptimo grado hay 15 alumnos más
que en quinto grado. La
tercera parte de los de quinto, la cuarta parte de los de sexto y
las dos terceras
partes de los de séptimo, estudian inglés. La
mitad de estos están en nivel avanzado.
En las clases de inglés de nivel
avanzado, hay en total 64 chicos de los tres grados. ¿Cuántos
chicos hay en quinto grado, cuántos en sexto y cuántos en séptimo?
3. En
cada punto hay que escribir un número del 1 al 12, sin
repeticiones, de manera que la suma
de los cuatro números
de cada una de las seis líneas sea
la misma.Ya hay cinco números
ubicados ( 1, 4, 6, 8 y
9).
Ubicar los siete números que faltan.
Segundo nivel
1. Un
productor almacena los 2007 kg de arroz que produce en cajas de 4 tamaños: pequeñas, de 1 kg;
medianas, de 2 kg; grandes, de 5 kg y muy
grandes, de 10 kg. En
las cajas grandes y las pequeñas, se almacenan,
en total, 657 kg. El
número total de cajas utilizadas es 348 y hay igual cantidad
de cajas grandes
que de cajas muy grandes.
¿Cuántas cajas de cada tamaño
utilizó?
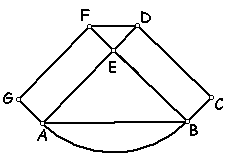2.
En la figura:
. El arco de circunferencia AB tiene centro E y
radio EB.
. El
triángulo ABE es isósceles y rectángulo en E.
. BCDE y AEFG son rectángulos
iguales.
. El área del rectángulo
BCDE es 6 veces el área del triángulo
DEF.
. El área
del sector circular AEB es 254,34 cm2.
¿Cuál es el área del polígono
ABCDFG?
3. Juan
tiene 11 varillas distintas para armar cuadrados.
Las longitudes de las varillas son: 1
cm, 2 cm, 3 cm, 4 cm , 5 cm , 6 cm, 7 cm,
8 cm, 9 cm, 10 cm y 11 cm.
No es obligatorio usar todas las
varillas para armar un cuadrado.
Dos cuadrados son distintos si para
alguno de sus lados se usan varillas
de distintas longitudes.
¿Cuántos cuadrados distintos puede
armar Juan?
Observación: Los cuadrados I)
, II)
y III)
se armaron utilizando las varillas:
I)
10 -
2 y 8 –
9 y 1 –
7 y 3
II)
8 y 2 -
10 -
3 y 7 -
1 y 9
III)
10 –
5, 3 y 2 - 6 y 4 –
9 y 1
I) y II) son el mismo
cuadrado,
II) y III) son
cuadrados distintos
Tercer nivel
1.
Aldo, Blas,
Carlos y Dani tienen, entre los cuatro, $
420.
Si entre Carlos y Dani le prestaran $
100 a Aldo y Blas juntos, entre
Aldo y Blas tendrían el triple del dinero que les quedaría a Carlos y Dani
juntos.
Si entre Aldo y Dani le prestaran $
106 a Blas y Carlos juntos,
entre Blas y Carlos tendrían el cuádruple
del dinero que les quedaría a Aldo y Dani juntos.
Si entre Aldo, Blas y Carlos le
prestaran $ 60 a Dani,
Dani tendría la mitad del dinero
que les quedaría a Aldo, Blas y Carlos, juntos.
¿Cuánto dinero tiene cada uno?
2.
Un
grillo recorre un camino recto señalizado con postes, saltando de poste en
poste.
Los postes están numerados, en forma
creciente, del 1 al 14.
Sale del poste que tiene el número 1
y llega al poste que tiene el número 14,
según estas reglas:
- Debe
moverse en el sentido creciente de la numeración.
- Debe
hacer por lo menos tres saltos.
- Del
poste que tiene el número 1 puede saltar a cualquier otro poste.
- A
partir de allí, sólo puede ir de un poste a otro si los números de ambos
postes tienen algún divisor común distinto de 1.
¿Cuántos recorridos distintos puede
hacer el grillo?
3. Juan
dibujó un triángulo rectángulo ABC con Â=
90°
, AB= 60 cm y
AC= 80 cm. Sobre
el lado AC marcó un punto D; por D trazó la paralela al lado AB
que corta al lado BC en el punto
E. Resultó
que DE = 24 cm y
que los triángulos ACE y
ABE tenían igual perímetro. ¿Cuál
es el perímetro del triángulo ABE?
¿Cuál es el área del triángulo
ABE?
