15º Olimpíada
Matemática Ñandú
Certamen Nacional - 2006
Primer nivel
1.
Al
concierto asistieron 120 personas entre hombres, mujeres y niños. Recaudaron $
1200 por la venta de entradas.
Los hombres pagaron $ 50, las mujeres pagaron $ 20 y los niños, $1.
El total de adultos que concurrieron era un tercio del número de niños.
¿Cuántos hombres, mujeres y niños estuvieron en el concierto?
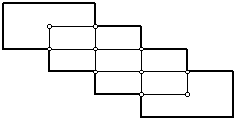
2. Superponiendo rectángulos iguales de cartulina, Camila arma la figura que se muestra.

En
cada rectángulo la base es el doble de la altura. Los
lados de los rectángulos superpuestos se
cortan en sus puntos medios.
El perímetro de la figura que se muestra es
de 30 cm.
a) Siguiendo este procedimiento, Camila
arma una figura con 10 de estos rectángulos. ¿Qué
perímetro tiene la figura que armó Camila?
b) ¿Podrá armar, con este procedimiento, una figura de 2006 cm de perímetro?
Si es posible, indica cuántos rectángulos debe utilizar. Si no es posible,
explica por qué.
3.
Fra
Con este procedimiento obtiene, cada vez, un número entero entre 3 y 50. Escribe
la lista de los números que puede obtener Francisco. Para
cada número de la lista, muestra alguna manera de obtenerlo.
Segundo nivel
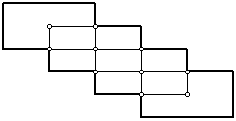
1. Superponiendo rectángulos iguales de cartulina, Clara arma una figura como la que se muestra.
Los
lados de los rectángulos superpuestos se cortan en sus puntos medios.
La figura que Clara arma con 10 de estos rectángulos tiene 248 cm2 de área.
¿Podrá armar, con este procedimiento, una figura de 2006 cm2 de área?
Si es posible, indica cuántos rectángulos debe utilizar. Si no es
posible, explica por qué.
2.
Con los dígitos
del 0 al 9, se quieren armar conjuntos de cuatro dígitos distintos de
modo que la suma de esos cuatro dígitos sea múltiplo de 5.
¿Cuántos conjuntos se pueden armar? Da todas las posibilidades.
3. En
Navidad, Aldo, Bruno, Carlos y Daniel recibieron cada uno un número distinto de
regalos. Además, se repartieron caramelos de manera que, cada chico, recibió
10 caramelos por cada uno de los regalos que recibieron los otros chicos y tuvo
que devolver 20 caramelos por cada regalo que él recibió. En total se
repartieron 390 caramelos. Al final, a Aldo no le quedaron caramelos, a Bruno le
quedaron 120 caramelos y a Carlos le quedaron el doble de caramelos que a
Daniel. ¿Cuántos
regalos se repartieron en total y cuántos regalos recibió cada uno de los
chicos?
1.
El banco tiene 4
empleados, cada uno de una categoría distinta: A, B, C y D. En
enero, el promedio de los sueldos de los cuatro empleados era $800. En
marzo, el de categoría A recibió un 20 % de aumento y el de categoría B
recibió un
30 % de aumento. El promedio de los sueldos de los cuatro fue entonces de $935. En
julio, los de categorías C y D recibieron un 25 % de aumento cada uno. El
promedio de los sueldos de los cuatro fue entonces de $997,50. En
setiembre, el de categoría C recibió un 20 % de aumento y su sueldo fue $900. ¿Cuál
era el sueldo de cada empleado en enero?
Observación: El promedio de 4 números es la suma de los mismos dividida por 4.
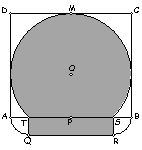
2. En la figura, ABCD y QRST son rectángulos, M es punto medio de CD, P es punto medio de ST. MO = MD, OP = PS, el arco ST está en la circunferencia de centro O y radio OM, el arco RB está en la circunferencia de centro S y radio RS. El arco AQ está en la circunferencia de centro T y radio QT. El perímetro de la parte sombreada es 214,72 cm.¿Cuál es el área de la parte no sombreada?
3. Apilando
pelotitas se arman pirámides de varios pisos.
Cada piso es de forma triangular.
La pirámide de 2 pisos tiene 1 pelotita en el piso más alto y 3 pelotitas en
la base.
La de 3 pisos tiene 1 pelotita en el piso más alto, 3 en el de abajo y 6 en la
base.
La de 4 pisos tiene 1 pelotita en el piso más alto, 3 en el de abajo, 6 en el
siguiente y 10 en la base.
Walter y Yago tienen cada uno 2006 pelotitas y siguiendo este método arma, cada
uno, la pirámide más alta que puede. Cada uno puede devolver las pelotitas que
le sobran o pedir hasta 100 pelotitas.Si se devuelve una pelotita, se descuenta
1 punto; si se pide una, se descuentan 10 puntos.
Walter armó su pirámide devolviendo algunas pelotitas; Yago, en cambio, pidió
algunas.
¿Cuántos pisos tiene la pirámide de Walter y cuántos la pirámide de Yago?
¿Cuál de los dos chicos perdió más puntos?
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |