14º Olimpíada Matemática Ñandú
Certamen Interescolar

26 de mayo 2005

 

Primer nivel

1. El sábado, la Sra. Juárez gastó $ 360 en la compra de ropa y zapatos. Gastó una cuarta parte en zapatos. Con el resto compró un pantalón a $ 85, una campera a $ 120 y un saco de lana. ¿Cuánto pagó por el saco?

 

2. La figura ACDE tiene 882 cm de perímetro.  ABDE es un rectángulo.  CD = 282 cm;  BC = BD;  AB es la mitad de BD

    ¿Cuál es el perímetro del triángulo BCD?

 

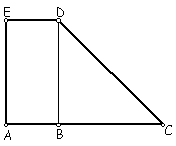
3. Dani tiene 6 lápices de distintos colores para regalar a dos amigos: Juan y Pedro.  Regala 3 lápices a cada uno.

     ¿De cuántas maneras puede regalarlos? Indica qué lápices regala a cada amigo.

 Segundo nivel

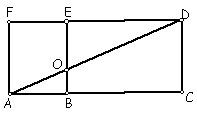
1. En la tienda, los pantalones de lana cuestan $ 70, los pantalones de algodón $ 50 y las remeras $ 12.  El sábado, tenían una promoción:  “Si compra un pantalón de lana, le regalamos una remera”.  Ese día recaudaron  $ 2540. Si habían vendido 34 pantalones y habían regalado 15 remeras, ¿cuántas remeras vendieron?

2. El rectángulo ACDF tiene 102 cm de perímetro.  BC = 24 cm  ,    CD= 15 cm   y    DO = 26 cm. El cuadrilátero BCDO tiene 70 cm de perímetro. El triángulo  ABO tiene 30 cm de perímetro. ¿Cuál es el perímetro de AOEF?  

 

3. En la vidriera de una casa de venta de ropa deportiva, deben vestir a dos maniquíes, uno con ropa de varón, otro con ropa de mujer. Les pueden poner equipos de color: verde, rojo o gris y zapatillas de color: blanco, negro o azul. Los dos maniquíes pueden tener sus equipos del mismo color pero deben  tener zapatillas de distinto color. ¿De cuántas maneras pueden quedar vestidos los dos maniquíes?

 

Tercer  nivel

1. En un monedero hay solamente monedas de 25 y de 50 centavos.  El número de monedas de 25 centavos es el triple del número de monedas de 50 centavos. Si se gastan 8 monedas de cada clase, ahora, la cantidad de monedas de 50 centavos es la quinta parte de la cantidad de monedas de 25 centavos. ¿Cuánto dinero había inicialmente en el monedero?

 

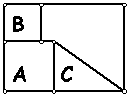
2. De una hoja rectangular se cortan tres pedazos como indica la figura.  A es un cuadrado de 144 cm2 área. B es un cuadrado de 81 cm2 área. C es un triángulo rectángulo de 102 cm2 área. ¿Cuál es el área del pedazo que sobra? 

   

3. Juan tiene un rompecabezas de 1200 piezas cuadradas de 1 cm de lado. Utilizando todas las piezas arma un rectángulo.  ¿Cuántos rectángulos distintos puede armar? Indica las longitudes de sus lados.  

¿Cuáles de estos rectángulos se pueden partir en cuadrados de 2 cm de lado?

 

 

Archivo de Enunciados Página Principal Olimpíada Matemática Argentina
   www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar