XIII Olimpíada Matemática Ñandú
Certamen Regional

2 de septiembre de 2004

Primer Nivel

1

Con los dígitos 1, 2, 3, 4, 5, 6, 7, 8 y 9 se arman todos los números de tres cifras que son múltiplos de 3 y tienen sus cifras distintas, ordenadas de mayor a menor.
¿Cuántos son? Escríbelos todos.

2

En la librería se pueden comprar 4 cuadernos por $10 o 1 cuaderno por $3. Esta semana se vendieron 120 cuadernos en total y se cobraron $320 por la venta de los cuadernos.
¿Cuántos cuadernos se vendieron de a 1 y cuántos cuadernos se vendieron de a 4?

3

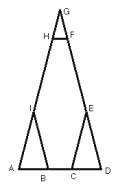
En la figura AG = 2AD; AG = GD y HG = GF. Los triángulos ABI y CDE se obtienen duplicando los lados del triángulo HFG.
AB = 2BC y EF = 2FG. El perímetro de BCEFHI es 108cm.
¿Cuál es el perímetro de ADG?

Segundo Nivel

1

Ale quiere guardar sus figuritas en cajas, de manera que en cada caja haya igual número de figuritas. Tiene menos de 1000 figuritas. Tiene que usar 7 cajas porque con menos cajas siempre le sobran tantas figuritas como el número de cajas que quiere usar disminuido en una unidad. Por ejemplo, si usa 3 cajas le sobran 2 figuritas.
¿Cuántas figuritas puede tener Ale? Da todas las posibilidades.

2

Por la compra e instalación de un equipo de aire acondicionado, Gabriela pagó $2502,90 en total. El gasto de instalación es del 8% del costo del equipo y sólo puede pagarse al contado. El equipo puede pagarse al contado o en 6 cuotas iguales y sin recargo. Si se paga al contado, sobre el precio del equipo hacen un 5% de descuento. Gabriela pagó al contado.
Si hubiera pagado el equipo en cuotas, ¿cuánto debería haber pagado por cada cuota?

3

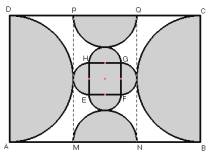
ABCD es un rectángulo. EFGH es un cuadrado. Todos los arcos son semicircunferencias.
BA = 3/2 BC; BM = BC; MN = NB.
PM es paralela a AD, y QN es paralela a BC. El perímetro de la zona blanca es 165,6cm.
¿Cuál es el área de la zona blanca?

Tercer Nivel

1

La sala del teatro tiene 240 asientos. En la función del domingo todos los asientos estaban ocupados. Las entradas cuestan $12 para mayores y $8 para menores, los invitados no pagan. Por venta de entradas para la función del domingo ingresaron $2640.
¿Cuántos mayores, cuántos menores y cuántos invitados hubo? Da todas las posibilidades

2

Se venden 140 naranjas, una parte ganando el 30% y el resto perdiendo el 20%.
Si al final no se gana ni se pierde, ¿cuántas naranjas se vendieron con ganancia?

3

Sobre una circunferencia de centro O, se marcan los vértices del dodecágono regular ABCDEFGHIJKL. Se dibuja el polígono de vértices ACFHJ. La longitud del arco AH que contiene al punto E es 65,94m.
¿Cuál es el área y cuál es el perímetro del polígono ACFHJ?

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar