13º Olimpíada
Matemática Ñandú
Certamen Nacional - 2004
Primer nivel
1.
Se
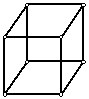
quieren colocar los números 1- 2 – 3 – 4 – 5 – 6 - 7- 8 en
los vértices del cubo, de modo que la
suma de los números que hay en los vértices de
cada una de las caras sea
siempre la misma.
Muestra cómo hacerlo.

2.
María tiene un
rompecabezas de piezas rectangulares, una pieza de cada tamaño. Ordenadas de
menor a mayor, la primera tiene 2 cm de base y 3 cm de altura; la segunda tiene
2 cm de base y 4 cm de altura; la tercera tiene 2 cm de base y 5 cm de
altura y así sucesivamente.
Las bases son todas de 2 cm y las alturas aumentan 1 cm cada vez. Las pone
en escalera una a continuación de otra, así:
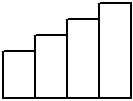
a)
Con las 100 primeras piezas arma una figura, ¿qué perímetro tiene esta
figura?
b) Poniéndolas en el mismo orden, ¿es posible que María arme una figura de
2004 cm de perímetro?
Si es posible, ¿cuántas piezas necesita? Si no es posible, explica
por qué.
3. En
febrero, un librero compró 120 cajas de diccionarios; por cada dos cajas recibió
un diccionario de regalo. Cada caja contiene una docena de diccionarios.
Durante el mes de marzo vendió las tres quintas partes de todos los
diccionarios que tenía, cada uno a un tercio más de lo que había pagado por
cada uno de los que compró. En
abril vendió los restantes diccionarios, cada uno a un tercio menos de lo que
había pagado por cada uno de los que compró. En
total ganó $ 5760. ¿Cuánto le había costado cada caja de diccionarios?
Segundo nivel
1. Un
arquitecto compra los cerámicos que necesita para una obra a dos proveedores
distintos, A y B.
A cada uno le compra artículos de primera y de segunda selección. El
proveedor A le cobra $40 el m2 de primera y el 10 % menos el m2 de segunda. El
proveedor B le cobra $30 el m2 de primera y el 20 % menos el m2 de segunda. El
arquitecto compra igual cantidad de m2 de primera que de segunda. Un tercio de
lo que le compra al proveedor B es de segunda. Por su compra paga $ 31000.
Si
le comprara, al proveedor A, de cada clase, la misma cantidad que le compró y,
al proveedor B, de cada clase, el doble de lo que le compró, gastaría
$ 39400. ¿Cuántos
m2 de cada clase compró a cada proveedor?
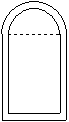
2. La
superficie de vidrio de una ventana está
formada por una pieza rectangular y una semicircular, como muestra la
figura.Esta superficie está ordeada por un marco de 2 cm de ancho.
La parte vidriada tiene altura igual al doble
de la base. El área de la parte vidriada es de 3028 cm2.
¿Cuál es la longitud del borde exterior?
3. Se
acomodan 2004 fichas rectangulares iguales formando una larga hilera.
Paso
a paso hay que sacar fichas de acuerdo con las siguientes reglas:
En el primer paso sólo se puede sacar una ficha.
En los pasos siguientes, se puede retirar una ficha o una ficha más que en el paso inmediato anterior.
Si se sacan varias fichas, éstas tienen que estar una al lado de la otra.
Cada vez que se sacan una o más fichas, debe haber una ficha en el lugar inmediato anterior una ficha en el lugar inmediato posterior de lo que se saca.
Por
ejemplo, en el primer paso no se pueden sacar ni la primera ni la última ficha.
¿Cuál es la menor cantidad de fichas que pueden quedar sobre la mesa?
Explica cómo lo hiciste.
1.
Para entrar al
nuevo hipermercado hay una cola de 2004 personas.
El Comité de Inauguración decide hacer salir de la fila a las personas que
ocupan los lugares 7;14; 21 y así cada 7; a cada una le regalan una orden de
compra.
Entre los que quedan, elige personas a intervalos regulares, las retira de la
fila y les obsequia, a
cada una, una lapicera.
De la nueva fila, a las personas que están ahora en los lugares 5; 10; 15; y así
cada 5, las retira de la fila y les permite participar en un sorteo.
Al final, quedan en la fila, 1223 personas. ¿Una de cada cuántas personas de
la segunda fila recibió una lapicera?
2.
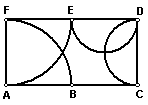
ACDF es un rectángulo de 96 cm de perímetro.
DE = EF
Los
arcos AE y BF son cuartos de circunferencias.
Los arcos CD y DE son semicircunferencias.
¿Cuál es el perímetro y cuál es el área de la zona sombreada?
3.
Carlos tiene
bolitas blancas y bolitas negras que guarda en cuatro cajas.
En cada tapa figura escrita qué parte, del total de bolitas de esa caja, son
blancas.![]() . Carlos tiene, en total más de 500 bolitas pero menos de 550.
. Carlos tiene, en total más de 500 bolitas pero menos de 550.
¿Cuántas bolitas negras y cuántas blancas hay? Explica por qué.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |