11º Olimpíada
Matemática Ñandú
Certamen Nacional - 2002
Primer nivel
1. Agustina tiene que pintar cada uno de los cuadraditos de esta tira
de
modo que haya 3 de un color, 2 de otro y 1 de otro color distinto de los
anteriores.
Puede usar los colores rojo, amarillo y verde. No puede pintar dos
cuadraditos vecinos de igual color.
¿De cuántas maneras distintas puede hacerlo?
2.
En una
competencia deportiva participan chicos de Argentina, Brasil, Paraguay y
Uruguay.
En total hay 432 chicos.El número de chicos de Paraguay es un tercio del número
de chicos de Uruguay. Si se duplicara el número de chicos de Argentina, en
total habría 588 chicos.
Si de Uruguay sólo viniera la mitad de los chicos, la cantidad de chicos de
Brasil y Uruguay sería 241.
¿Cuántos chicos de cada país participan en esa competencia?
3. Lucía
tiene piezas de cartón todas iguales entre sí. Cada pieza es un triángulo de
lados iguales. Cada lado mide un número entero de centímetros.
Si bordea todos los lados de todas las piezas de cartón con cinta, de un rollo
de 2002 cm le sobran 4 cm.
¿Cuántas piezas de cartón puede tener Lucía? Da todas las posibilidades e
indica, en cada caso, cuánto mide el lado.
Segundo nivel
1.
Un
librero compró al comienzo del mes, 60 ejemplares de cada uno de los tres tomos
de un libro de cuentos por $ 2640. La semana pasada compró 40 ejemplares del
tomo 1 y 40 del tomo 2 con un 20 % de descuento por $ 864. Esta
semana compró 45 ejemplares del tomo 2 y 45 del tomo 3 con un 10 % de
descuento por $ 1296. ¿Cuál
es el precio de cada tomo sin el descuento?
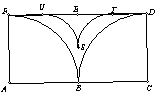
2. En
el rectángulo ACDF: AC = 2 AF, FE = ED, S es el punto de
intersección de las diagonales de ACDF, U es el punto medio de FE,
T es el punto medio de ED. 
es
un arco de circunferencia de centro A, 
es
un arco de circunferencia de centro C. P es el punto de intersección de las
diagonales de ABEF, Q es el punto de intersección de las diagonales de
BCDE, 
es
un arco de circunferencia de centro P, 
es
un arco de circunferencia de centro Q.
El perímetro de la región sombreada es de 51,39 cm; calcula su área.
3. Esteban
tiene 4 bolitas rojas, 4 bolitas azules y 4 cajas: una de madera, una de vidrio,
una de
cartón y una de lata. Quiere
guardar todas las bolitas de modo que ninguna caja quede vacía. Si
en una caja pone más de una bolita, no quiere que sean todas del mismo color.
¿De cuántas maneras puede guardar las bolitas en las cajas?
1.
En el cuadrilátero
ABCD, de 84 cm de perímetro,
, 
,
AD = AB , BC =
.
¿Cuál es el área del cuadrilátero ABCD?
2. En
la inauguración de los Juegos Olímpicos desfilaron todos los
participantes. El organizador quería formarlos en filas iguales. Intentó hacer
filas de 11 participantes pero no le quedaban iguales. Si ponía 10
participantes por fila le quedaba, al final, una fila de 9. Con
filas de 9, le quedaba una fila de 8. Probó con filas de 7; 6; 5; 4; 3 e
incluso 2, pero en cada una de estas pruebas, le quedaba un lugar libre
en la última fila. Si
el número de participantes no pasaba de los 7000, ¿cuántos eran?
3.
En el parque de
diversiones van a pintar los 6 autitos de la calesita.
Cada autito se pintará de un solo color. Se pueden usar todos o algunos de los
siguientes colores: rojo, negro, blanco, verde. ¿De cuántas maneras se pueden
pintar los 6 autitos, con la condición de que autitos vecinos queden de
distinto color?
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |