X Olimpíada
Matemática Ñandú
Certamen Nacional
24 al 26 de noviembre de 2001
Primer nivel
1
Esteban tiene más de 350 caramelos.
Hace paquetes de caramelos, poniendo en cada paquete la misma cantidad de caramelos. Si pone 2 ó 3 ó 4 5 ó 6 caramelos en cada paquete siempre le sobra un caramelo En cambio, si pone 7 caramelos en cada paquete no le sobra ningún caramelo.
¿Cuál es la menor cantidad de caramelos que puede tener Esteban?
2
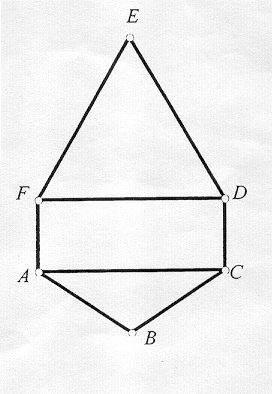
En la figura, ABC es un triángulo isósceles, DEF es un triángulo equilátero y ACDF es un rectángulo.
El perímetro del hexágono ABCDEF es 126 cm, el perímetro del pentágono ACDEF es 120cm y el perímetro del triángulo ABC es 70 cm. ¿Cuál es la longitud de cada uno de los lados del hexágono ABCDEF?
3
Aldo y Bruno juntan figuritas.
Aldo tiene 3 figuritas distintas y Bruno tiene 8 figuritas distintas, todas distintas de las de Aldo.
Quieren cambiar figuritas de modo que Aldo tenga siempre 3 figuritas y Bruno tenga siempre 8 figuritas.
¿De cuántas maneras pueden hacerlo?

Segundo nivel
1
El Sr. Dulce elabora caramelos de 3 gustos:
chocolate, miel y limón.
Los de chocolate los vende en bolsas de 100g a $2 cada bolsa.
Los de miel los vende en bolsas de 1/4 kg a $ 4 cada bolsa.
Los de limón los vende en bolsas de 1/2 kg a $6 cada bolsa.
El mes pasado vendió en total 244 kg de
caramelos, por $ 3600.
Por la venta de los caramelos de chocolate obtuvo el 25% de lo
que obtuvo por la venta de todos los caramelos de miel y limón.
¿Cuántos kilos de caramelos de cada gusto vendió el Sr. Dulce el mes pasado?
2
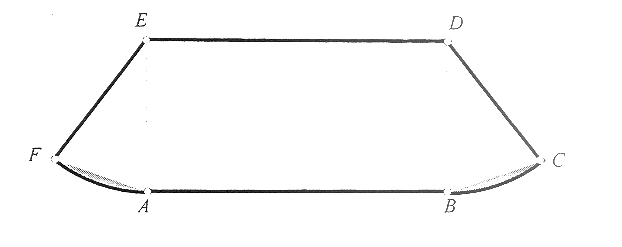
ABDE es un rectángulo. AB = 2 BD . Los triángulos BCD y AEF son iguales. AF es un arco de circunferencia de centro E y radio EA. BC es un arco de circunferencia de centro D y radio DB.
En el triángulo BCD, el ángulo BCD es el doble del ángulo CDB.
El perímetro de la figura es 87,08 cm. El área de la zona sombreada es 5,84 cm2 ¿ Cuál es el área de la zona no sombreada?
3
Coloca los números:
1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11- 12 - 13 - 14 - 15
uno en cada casilla de la cuadrícula de modo que las sumas de los números de cada una de las 5 columnas sean iguales entre si y las sumas de los números de cada una de las 3 filas sean iguales entre sí.

Tercer nivel
1
Ada y Bea deben recorrer 60 km para ir al pueblo. Ada camina a 5 km/h y Bea camina a 6 km/h.
Tienen una bicicleta en la que sólo puede andar una por vez, a 10 km/h.
Ada empieza el camino en bicicleta, al cabo de cierto tiempo deja la bicicleta y sigue a pie. Cuando Bea llega al lugar donde Ada dejó la bicicleta, deja de caminar y empieza a andar en bici.
Llegan a la mitad del cámino al mismo tiempo, allí descansan media hora.
Repiten después la misma combinación de marcha y bicicleta y llegan juntas al final del trayecto.
¿A qué hora llegarán a destino si salen juntas a las 6 de la mañana?
2
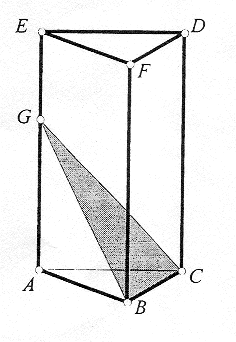
El cuerpo de la figura es un prisma recto de
base triangular.
G es un punto de la arista AE.
GE = 9 cm
AG = 16 cm
9C = 14 cm.
El área del triángulo BCG es 140 cm2.
¿Cuál es el volumen del prisma?
3
Un triángulo equilátero se puede partir en triangulitos equiláteros iguales como se ve en los ejemplos de la figura.
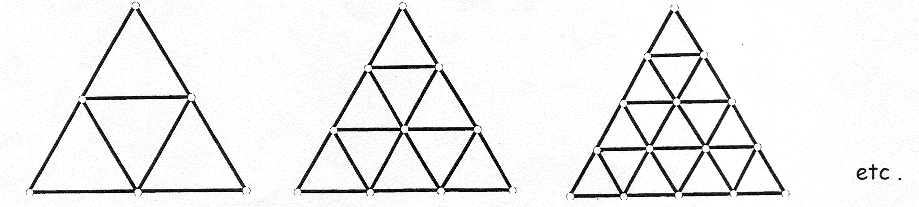
Dibujo un triángulo equilátero de 2001 cm de perímetro y quiero partirlo en triangulitos equiláteros iguales de modo que el lado de cada triangulito mída un número entero de cm. ¿En cuántos triangulitos iguales quedará partido el triángulo que dibujo? Da todas las posibilidades.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |