28º Olimpíada
Matemática Argentina
Certamen Intercolegial
26 de mayo de 2011
PRIMER NIVEL
1. Franco rindió un examen de tres partes, una de 40 preguntas, la siguiente de 30 preguntas y la tercera de 90 preguntas. En la primera parte respondió correctamente el 50% de las 40 preguntas, en la segunda respondió correctamente el 60% de las 30 preguntas y en la última respondió correctamente el 80% de las 90 preguntas.
Calcular qué porcentaje de respuestas correctas obtuvo Franco en todo el examen.
2. En una caja hay 250 bolitas azules y 220 bolitas rojas. Fuera de la caja hay muchas bolitas con esos mismos dos colores. Contamos 1 (una) movida cada vez que retiramos una bolita de la caja o cada vez que agregamos una bolita a la caja. Determinar la menor cantidad de movidas que hay que hacer para que la fracción entre la cantidad de bolitas azules en la caja y la cantidad de bolitas rojas en la caja sea igual a 4/3. Dar las cantidades de bolitas de cada color que quedaron en la caja.
3. Sea ABCD un trapecio de bases AB y CD , con AB > CD , tal que los lados AD , DC y CB son iguales y además el lado AB es igual a la diagonal AC . Calcular las medidas de los ángulos del trapecio.
SEGUNDO NIVEL
1. Gastón quiere numerar las páginas de un cuaderno. Para ello tiene gran cantidad de autoadhesivos con los dígitos 0, 1, 3, 4, 5, 6, 7, 8 y 9, pero sólo tiene 22 con el dígito 2. Determinar hasta que página puede numerar.
2. Un profesor tomó un examen a sus 36 alumnos, que obtuvieron en promedio 13 puntos. El promedio obtenido por los 15 primeros alumnos de la lista fue de 11 puntos y el promedio de los últimos 18 fue de 15 puntos. Si las notas obtenidas por los tres alumnos restantes son tres números enteros consecutivos, calcular esas tres notas.
3. Sea ABCD un cuadrado de lados AB , BC , CD y DA . Dos rectas r y s, exteriores al cuadrado y paralelas entre sí, pasan por A y C , respectivamente. La perpendicular p a estas dos rectas, trazada por B , corta a r en E y a s en F . Si BE = 5 y BF = 7, calcular el área del cuadrado ABCD .
| TERCER NIVEL |
|
|
|
t |
o |
r |
r |
e |
|
|
|
r |
e |
t |
o |
+ |
|
e |
r |
r |
o |
r |
|
|
|
t |
o |
r |
o |
|
|
|
o |
t |
r |
o |
|
|
|
|
4 |
5 |
8 |
7 |
5 |
|
1. En la siguiente suma, cada letra representa un dígito distinto (de 0 a 9).
Se sabe además que no hay acarreo, es decir, la suma en cada una de las cinco columnas es menor que 10, y que está permitido que el primer dígito de la izquierda sea igual a cero.
Reemplazar cada letra por el dígito correspondiente.
|
2. En una base de numeración desconocida, la siguiente expresión es correcta:
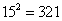
Escribir 2011 en esa base.
3. En el cuadrado ABCD de lado 3 se marcaron los puntos
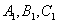y
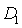en los lados AB, BC, CD y DA, respectivamente, de modo que
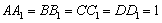y los puntos
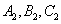y
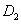en los lados DA, AB, BC y CD, respectivamente, de modo que
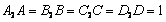.Sea KLMN el cuadrado determinado por las rectas
,
,
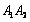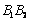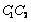y
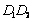
Calcular
|
|
