21º Olimpíada Matemática Argentina
Certamen Regional

9 de septiembre de 2004

Primer nivel

1

La ley pirata establece que para repartir las monedas de un tesoro el capitán debe elegir un grupo de piratas y repartir equitativamente las monedas entre los piratas elegidos hasta que no haya suficientes para darle una más a cada uno. Las monedas sobrantes son la parte del capitán. Morgan debe repartir un tesoro con menos de 1000 monedas de oro. El sabe que si elige 99 piratas se quedará con 51 monedas y si elige 77 piratas le corresponderán sólo 29 monedas.
Determinar cuántos piratas debe elegir Morgan para quedarse con la mayor cantidad de monedas respetando la ley pirata, y para esa cantidad de piratas, cuántas monedas le corresponden a Morgan.
ACLARACIÓN: Los piratas elegidos deben recibir por lo menos una moneda cada uno.

2

Nico debe elegir tres números enteros distintos entre 1 y 20 inclusive de modo que al multiplicar los tres números se obtenga un múltuplo de 4.
Calcular cuántas maneras tiene Nico de elegir sus tres números.
ACLARACIÓN: Dos elecciones que tienen los mismos tres números no importa en qué orden, son iguales.

3

En un trapecio ABCD de base mayor AB, base menor DC y lados no paralelos BC y DA, sea K el punto del lado BC tal que BK = 1/3 BC. Se traza por K la recta paralela a DA que corta a AB en L.
Si BL = CD y el área del trapecio ABCD es 20, calcular el área del triángulo ADL.

Segundo Nivel

1

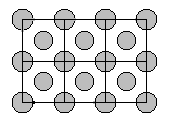
En un tablero cuadriculado de m x n se ubica una ficha en el centro de cada casilla y una ficha en cada vértice de la cuadrícula hasta que no quede lugar para más fichas (en la figura se muestra el tablero de 2 x 3 con sus 18 fichas).
Hallar las dimensiones m y n del tablero de m x n si se utilizan exactamente 500 fichas. Dar todas las posibilidades.

2

Fabio debe escribir una sucesión de números naturales.
El primer número lo elige Fabio entre 1 y 2004 inclusive, y a partir de alli, cada nuevo número se obtiene del anterior de acuerdo con la siguiente regla: si el anterior es impar, le suma 1, si el anterior es par, lo divide por 2. El proceso se detiene cuando se obtiene por primera vez el 1. Por ejemplo, si Fabio elige el primer número igual a 10, la sucesión será: 10, 5, 6, 3, 4, 2, 1, que tiene 7 números.
El objetivo de Fabio es lograr que su sucesión tenga la mayor cantidad posible de números. Determinar cuál es la máxima cantidad de números que puede tener la sucesión de Fabio y hallar un número inicial que le permita lograr una sucesión con esa cantidad máxima de números.

3

En el cuadrado ABCD de lado 6, sea M el punto medio del lado AD y N el punto medio del lado AB. La diagonal BD corta a CN en K y a CM en L.
Calcular el área del cuadrilátero KLMN.

Tercer Nivel

1

Un programa de computadora genera una sucesión de 2004 números, de acuerdo con la siguiente regla: el primer número es 1, y a partir de allí, luego de generar el número x, el siguiente número que genera es igual a x + 1/[x].
Los primeros números de la sucesión son 1; 2; 5/2; 3; ... ; pues ...
Determinar cuál es el último número que genera el programa.
ACLARACIÓN: Los corchetes indican la parte entera del número.

2

Se suman las 102 potencias de 7 desde 7⁰ = 1 hasta 7¹⁰¹:

3

Dado un triángulo ABC rectángulo en C, con AC/BC = 3, sea O el punto medio de la hipotenusa AB.
Se traza por O la perpendicular a AB que corta al cateto AC en P; se traza por P la paralela a AB que corta al cateto BC en Q y se traza por Q la perpendicular a AB que corta a AB en R.
Calcular PQ/RQ

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar