22º Olimpíada Matemática Argentina
Certamen Intercolegial

9 de junio de 2005

1. Hacer la lista de todos los enteros positivos de tres o más dígitos tales que cada par de dígitos consecutivos sea un número de dos dígitos que es cuadrado perfecto. Por ejemplo, 164 es un número de la lista, porque 16=4² y 64=8², pero 1645 no está en la lista porque 45 no es un cuadrado perfecto y 381 no está en la lista porque 38 no es un cuadrado perfecto.

2. En los vértices de un cubo hay que escribir con azul los números enteros de 1 a 8 inclusive, sin repeticiones. A continuación, en cada arista se escribe con rojo la diferencia de los números azules de sus dos extremos (el mayor menos el menor). Distribuir los números azules para que la cantidad de números rojos distintos sea la menor posible.

3. Dado un triángulo equilátero ABC, sean P y Q exteriores al triángulo tales que BQ corta al lado  

AC, CP corta al lado AB, AP=AQ=AB y . Calcular .

1. Consideramos el conjunto de los 17 primeros enteros positivos, {1,2,3,...,17}. Hay que elegir dos números de este conjunto tales que la multiplicación de esos dos números sea igual a la suma de los restantes 15 números.

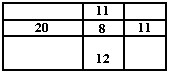
2. Un rectángulo se dividió en 9 rectángulos más pequeños mediante paralelas a su lados. En 5 de esos rectángulos pequeños se indica el perímetro. Calcular el perímetro del rectángulo inicial.

3. En un triángulo acutángulo ABC sea D en el lado BC tal que AD BC y E en el lado AC tal que BE AC. Si , AB=15 y AE=9, calcular la medida de AD.

1. Un arqueólogo ha descubierto que una antigua civilización usaba 5 símbolos para representar los números: . Estos símbolos corresponden en algún orden a los dígitos 0, 1, 2, 3 y 4. De este modo, cuando escriben  representan un número en base 5:

.

El arqueólogo sabe que los siguientes tres números son consecutivos, ordenados de menor a mayor:

,  y .

Hallar el valor de cada símbolo y cuáles son los tres números consecutivos.

2. En la pantalla de la computadora hay inicialmente un rectángulo de 21 milímetros de ancho y 33 milímetros de alto. Cada vez que se aprieta la tecla “+”, el ancho aumenta 2 milímetros y el alto aumenta 1 milímetro. Determinar cuántas veces hay que apretar la tecla “+” para que el área del rectángulo de la pantalla sea 25 veces el área del rectángulo inicial.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar