XVIII Olimpíada
Matemática Argentina
Certamen Intercolegial
17 de mayo de 2001
| primer nivel |
1
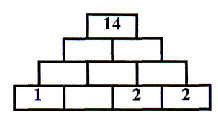
En el tablero de la figura hay cuatro casillas ocupadas.

Escribir en cada una de la seis casillas vacías un número (no necesariamente entero) de modo que una vez completo el tablero con los 10 números, se verifique que el número escrito en cada casilla sea igual a la suma de los dos números escritos en las dos casillas sobre las que está apoyada.
2
Hallar todos los números de cuatro cifras 1a7b que son múltiplos de 15. (a y b son dígitos no necesariamente distintos.)
3
En una circunferencia de centro O están marcados los puntos A, B y C, siguiendo el sentido horario, tales que AOB < BOC y AOC = 76°. Se marcan en la circunferencia M, N y P tales que OM es la bisectriz de AOB, ON es la bisectriz de BOC y OP es la bisectriz de MON . Si BOP = 5°, hallar la medida del ángulo BOC .
| segundo nivel |
1
Carlos escribe la lista de todos los números naturales menores que 10000 que tienen exactamente dos dígitos
1 consecutivos. (Por ejemplo, 113, 5112, 1181 están en la lista de Carlos, pero 1312, 2111 no están en la lista de Carlos.) Hallar cuántos números tiene la lista de Carlos.2
El
triángulo ABC tiene A = 67° y B= 79°. Sean P en el lado AB, Q en el lado BC y R en el lado CA tales que los ángulos APR = BPQ, BQP = CQR y CRQ = ARP . Hallar las medidas de los ángulos del triángulo PQR. NO VALE MEDIR.3
Hallar
el menor número natural que satisface las siguientes tres condiciones simultáneamente: tiene resto 24 en la división por 57; tiene resto 73 en la división por 106 y tiene resto 126 en la división por 159.
| tercer nivel |
1
En la siguiente configuración de nueve círculos hay seis maneras de elegir cuatro círculos de modo que los centros de los cuatro círculos sean los vértices de un cuadrado.

Distribuir los números 1, 2, 3, 4, 5, 6, 7, 8 y 9, uno en cada círculo, de modo que para cada uno de los seis cuadrados mencionados, la suma de los cuatro números escritos en los cuatro círculos correspondientes a sus vértices sea siempre la misma.
2
De un trapecio isósceles se sabe que sus diagonales son perpendiculares y su área es igual a 98. Hallar la altura del trapecio.
3
Hallar todos los cuadrados perfectos menores que 100000 que son
iguales a un cubo perfecto multiplicado por 3/2.ACLARACION: Los cuadrados perfectos son los números que se obtienen al elevar al cuadrado los números naturales y los cubos perfectos son los números que se obtienen al elevar al cubo los números naturales.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |