XV Olimpíada
Matemática Argentina
Certamen Nacional
Noviembre de 1998
| primer nivel |
1
Leandro elige un número natural n y hace lo siguiente:
calcula a = n2 + 5 ;
calcula b = (n+1)2 + 5 ;
halla el máximo común divisor entre a y b y anota dicho máximo común divisor en el pizarrón.
¿Cuál es el número más grande que puede anotar?
2
Durante un operativo, la policía encontró1001
monedas en apariencia todas iguales, junto con una nota que
decía que 501 monedas eran auténticas y las demás falsas, y
que cada moneda falsa era un gramo más liviana que cada moneda
auténtica. Para clasificar las monedas, vino un experto con una
balanza de dos platillos que no sólo indica en que platillo se
encuentra el objeto más pesado, sino que además indica la
diferencia entre los pesos de los objetos de cada uno de los
platillos.
El experto dice que cualquiera sea la moneda que elija la
policía, él siempre puede asegurar si es auténtica o falsa
utilizando una sola vez la balanza.
3
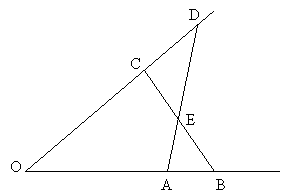
En los lados del ángulo de vértice O se consideran los puntos A, B, C, D (ver figura). Sea E el punto de intersección de los segmentos AD y BC. Se traza por C la recta paralela a AB y se traza por A la recta paralela a CD. Sea F el punto de intersección de las dos rectas trazadas. Demostrar que
Área (OAEC) = Área (BFDE)
4
Cuatro autos, A, B, C, D, viajan a velocidades constantes por la misma ruta, pero D viaja en dirección contraria a los otros tres. El auto A pasa a los autos B y C a las 8:00 hs y 9:00 hs respectivamente, y se cruza con el auto D a las 10:00 hs. El auto D se cruza con los autos B y C a las 12:00 hs y 14:00 hs, respectivamente. Determinar a qué hora el auto B pasó al auto C.
5
Dados los segmentos
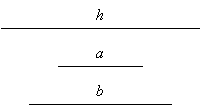
construir con regla y compás un triángulo ABC
de manera tal que, si D es el pie de la altura correspondiente al
vértice C, entonces CD = h, AC-AD = a, BC-BD =
b.
Indicar los pasos de la construcción y explicar porqué la
construcción realizada satisface las condiciones del problema.
6
Se tiene un tablero cuadrado cuadriculado de 5x5
y fichas rectangulares de 2x1; cada ficha cabe exactamente en dos
casillas adyacentes del tablero.
Las fichas se colocan en el tablero ocupando exactamente dos
casillas adyacentes. El tablero está dominado cuando ya
no hay espacio para colocar más fichas.
¿Cuál es el menor número de fichas que se debe colocar para
dominar el tablero? Explicar por qué es imposible dominar el
tablero con menos fichas.
| segundo nivel |
1
Hallar un número natural n tal que su cuadrado tenga
202 dígitos: los primeros 100 (desde la izquierda) todos iguales
a 1, los siguientes 100 todos iguales a 2 y los dos últimos,
desconocidos. Es decir, 
.
2
La compañía Cargo Sur recibió un pedido para transportar varios containers con un peso total de 50 toneladas. Cada container pesa a lo sumo una tonelada, pero no hay información acerca de cuál es la cantidad de containers; no se sabe si los containers son todos iguales ni se sabe cuánto pesa cada uno. La carga total será distribuida en varios camiones, cada uno con capacidad máxima para 5 toneladas, que harán un viaje cada uno. ¿Cuál es el menor número de camiones que debe enviar la compañía para garantizar que toda la carga será transportada como corresponde?
3
Los triángulos A1B1C1 y A2B2C2
tienen lados paralelos: A1B1||A2B2,
B1C1||B2C2, C1A1||C2A2
y el triángulo A2B2C2 está
contenido en el interior del triángulo A1B1C1.
Un tercer triángulo ABC está inscrito en A1B1C1
y circunscrito a A2B2C2, es
decir, los puntos A, B, C pertenecen al interior de los segmentos
B1C1, C1A1, A1B1
y los puntos A2, B2, C2
pertenecen al interior de los segmentos BC, CA, AB,
respectivamente.
Si el área de A1B1C1 es 63 y el
área de A2B2C2 es 7, hallar el
área de ABC.
4
Matías y Fernando pasaron la noche en los refugios A y B, respectivamente. A la mañana siguiente, Matías camina hacia B y Fernando hacia A; los dos van a velocidades constantes, y los dos recorren el mismo sendero que pasa por un bosque. Matías salió de A a las 8:00 hs y llegó a B a las 11:00 hs; Fernando salió de B a las 8:30 hs y llegó a A a las 11:00 hs. Los dos entraron en el bosque a la misma hora (cada uno siguiendo su dirección), y uno de ellos salió del bosque 3 minutos antes que el otro. ¿A qué hora salió Matías del bosque?
5
En el pizarrón había dibujado un cuadrilátero ABCD, con BC = CD = DA, que tenía marcados los puntos medios M, N, P de esos tres lados iguales. Se borró toda la figura, menos los puntos M, N y P. Reconstruir el cuadrilátero, indicando los pasos de la construcción.
6
Cada casilla de un tablero de 8x8 está coloreada de blanco o
de negro. Cada operación permitida consiste en elegir
en el tablero cualquier rectángulo de 3x4 o de 4x3 que cubra
exactamente 12 casillas y cambiar simultáneamente los colores de
esas 12 casillas (las blancas pasan a negras y las negras pasan a
blancas).
Diremos que una coloración es buena si es posible,
mediante una sucesión de operaciones permitidas, obtener a
partir de ella un tablero que tiene todas las casillas blancas.
En caso contrario, la coloración es mala.
Demostrar que el número de coloraciones malas es mayor
o igual que 15 veces el número de coloraciones buenas.
| tercer nivel |
1
Jorge escribe una lista con una cantidad par de números enteros, no todos iguales a 0 (puede haber números repetidos). Demostrar que Martín puede tachar un número de la lista, a su elección, para que a Jorge le sea imposible separar los restantes números en dos grupos de modo tal que la suma de todos los números de un grupo sea igual a la suma de todos los números del otro grupo.
2
Sea un cuadrilátero ABCD que posee una circunferencia inscrita y sean K, L, M, N los puntos de tangencia de los lados AB, BC, CD y DA, respectivamente. En cada uno de los triángulos AKN, BLK, CML y DNM se considera el punto de intersección de las alturas (es decir, el ortocentro del triángulo). Demostrar que estos cuatro puntos son los vértices de un paralelogramo.
3
Dados dos enteros m
2 y n2 consideramos dos tipos de sucesiones de
longitud m.n formadas exclusivamente por 0 y 1:
Las sucesiones de TIPO 1 son todas las que verifican las
siguientes dos condiciones:
Las sucesiones de TIPO 2 son todas las que verifican las siguientes dos condiciones:
Demostrar que la cantidad de sucesiones del tipo 1 es igual a la cantidad de sucesiones del tipo 2.
4
Determinar todos los valores posibles de la expresión
x - [ x/2 ] - [x/3 ] - [ x/6 ]
al variar x en los números reales.
ACLARACIÓN: Los corchetes indican la parte entera del número
que encierran.
5
Sea ABC un triángulo isósceles y rectángulo de hipotenusa
AB = 
. Determinar las posiciones de los puntos
X, Y, Z en los lados BC, CA, AB, respectivamente, de modo que el
triángulo XYZ es isósceles, rectángulo, y de área mínima.
6
Dados n números reales no negativos, n3,
tales que la suma de los n números es menor o igual que
3 y la suma de los cuadrados de los n números es mayor
o igual que 1, demostrar que entre los n números se
pueden elegir tres cuya suma es mayor o igual que 1.
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |