XV Olimpíada
Matemática Argentina
Certamen Intercolegial
2 de Julio de 1998
| primer nivel |
1
El triángulo ABC tiene ^C=90°, AC=20, AB=101. Sea D el punto medio de CB. Hallar el área del triángulo ADB.
2
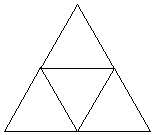
Un triángulo equilátero se divide en cuatro triangulitos
equilateros iguales (ver figura). Quedan determinados 9 segmentos
que son lados de triangulitos.
Distribuir los números 1, 2, 3, 4, 5, 6, 7, 8, 9 en los lados de
los triangulitos, sin repeticiones, de modo que la suma de los
tres números correspondientes a cada triangulito sea siempre la
misma.

3
Con los dígitos1, 2, 3, 4, 5, 6, formar un número de seis cifras distintas abcdef tal que el número de tres cifras abc sea múltiplo de 4, el número de tres cifras bcd sea múltiplo de 5, el número de tres cifras cde sea múltiplo de 3 y el número de tres cifras def sea múltiplo de 11.
| segundo nivel |
1
En una recta se marcan los puntos A y B tales que AB=5cm. Una pulga se mueve sobre la recta y en cada salto se desplaza 1cm a derecha o a izquierda. La pulga quiere ir de A hasta B en exactamente 9 saltos. ¿De cuántas maneras puede hacerlo?
2
Sea ABCD un cuadrado de lado 28. Se considera el punto P interior al cuadrado y el punto E en el lado CD tales que PE es perpendicular a CD y AP=BP=PE. Hallar AP.
3
Pablo colecciona monedas de España, Francia y Grecia. Tiene
monedas de 5 centavos, de 10 centavos y de 50 centavos, y tiene
en total menos de 100 monedas.
El lunes vendió tres monedas de Francia y compró tres de
España, pero con los mismos valores que tenían las que vendió.
El martes vendió seis monedas de 10 centavos y compró seis
monedas d 5 centavos pero exactamente de los mismos países que
las que vendió.
En su nueva colección:
¿Cuántas monedas de cada país tenía la colección inicial de Pablo y cuántas monedas de cada valor tenía la colección inicial de Pablo?
| tercer nivel |
1
Hallar todos los números enteros n tales que (n+98)/(n+19) es un número entero.
ATENCIÓN: Los números enteros son {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}.
2
En el triángulo isósceles ABC (con AB=AC), sean P y Q en AB
y AC, respectivamente, tales que PQ es paralelo a BC. La altura
desde A intersecta a PQ en O y a BC en M.
Si AP=64 y ![]() , hallar AB.
, hallar AB.
3
Sean x, y, números reales tales que x + y = 26, x3 + y3 = 5408. Hallar x2 + y2.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |