Primer nivel

1. Daniela, Iván, Laura y Matías escriben números naturales de cinco dígitos distintos formados por los dígitos 1, 2, 3, 4, y 5.
Daniela hace la lista de todos los que tienen la primera cifra igual a 1.
Iván hace la lista de todos los que tienen las dos primeras cifras formadas por los dígitos 1 y 2 en cualquier orden.
Laura hace la lista de todos los que tienen las tres primeras cifras formadas por los dígitos 1, 2 y 3, en cualquier orden.
Matías hace la lista de todos los que tienen las cuatro primeras cifras formadas por los dígitos 1, 2, 3 y 4, en cualquier orden.
Hay números naturales de cinco cifras distintas, formados por los dígitos 1, 2, 3, 4 y 5, que no figuran en ninguna de las cuatro listas. ¿Cuántos son los números que no figuran en ninguna lista?

2. Sean ABC un triángulo (A>90o) y M el punto medio del lado BC. Si <BAM=90o, AB=35 y AC=77, calcular BC.

3. Decidir si es posible que un conjunto de cinco números naturales distintos tenga la siguiente propiedad:

"Para cada par de números del conjunto, al multiplicar los dos números se obtiene un múltiplo de la suma de los dos números".

Si la respuesta es sí, indicar un conjunto con la propiedad.
Si la respuesta es no, explicar el porqué.

Segundo nivel

1. Hallar todos los números naturales x, y, z tales que

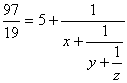
2. Sean ABC un triángulo, E el punto medio AC y O el punto medio de BE. La recta AO intersecta al lado BC en D. Si AO=12, calcular OD.

3. Diremos que un número natural es travieso si su desarrollo binario tiene un cantidad impar de dígitos 1; 6 no es travieso porque su desarrollo binario es 110 que tiene un cantidad par de dígitos 1.
Determinar la cantidad de números traviesos que son menores o iguales que 1997.

Tercer nivel

1. Hallar todos los números naturales n tales que [n2/5] es un número primo.
ACLARACIÓN: Los corchetes indican la parte entera del número que encierran.
Por ejemplo, [100/5]=20, [121/5]=4, etc.

2. Hallar el último dígito antes de la cola de ceros del número

19! + 20! + 21! + ... + 96! + 97!.

ACLARACIÓN: La notación n! indica el producto de todos los números entre 1 y n.
Por ejemplo, 4!=4.3.2.1=24, 10!=10.9.8.7.6.5.4.3.2.1=3628800, etc.

3. Los cuatro lados de un trapecio isósceles son tangentes a una circunferencia y los puntos de tanencia son vértices de un cuadrilátero cuya área es 4/9 del área del trapecio.
Si a es la base menor del trapecio y b es la base mayor del trapecio, hallar a/b.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar